一个东西写到10,总会多少有点成就感...只是不知道已经磨掉了多少人的耐心了呢?
此外这节公式密集,大家看着办吧...
-----------笔记开始------------
继续上一讲,先说说EM算法。
MM、EM和GMM
1. MM(混合模型)
(1) 定义: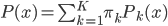 ,其中
,其中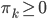 ,
,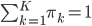 ,构成一个离散分布。同时有
,构成一个离散分布。同时有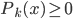 ,且
,且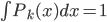 ,
,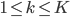 。
。
(2) 隐变量
我们有数据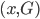 ,同时依据条件概率分布,有
,同时依据条件概率分布,有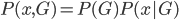 。记
。记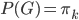 ,则
,则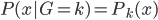 ,其中
,其中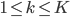 。
。
则有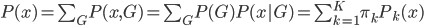 为x的边际分布。
为x的边际分布。
(3) GMM(正态混合模型)
当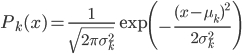 ,
,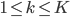 ,我们有
,我们有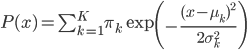 ,且
,且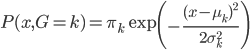 ,
,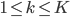 。
。
(4) 对数似然函数和最大似然估计
对数似然函数写为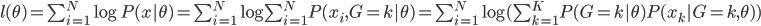 。则我们要求的就是
。则我们要求的就是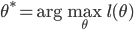 ,其中
,其中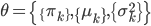 。
。
2. EM算法 (expectation maximum,期望最大方法)
(1) 迭代方法: 给定起始值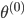 ,迭代出
,迭代出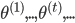 。那么问题就是,如何在已知
。那么问题就是,如何在已知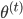 的情况下,求
的情况下,求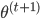 ?
?
(2) E1步:求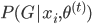 。函数形式已知,故可以求各种条件概率什么的。所以有:
。函数形式已知,故可以求各种条件概率什么的。所以有:
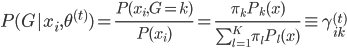 。
。
E2步:计算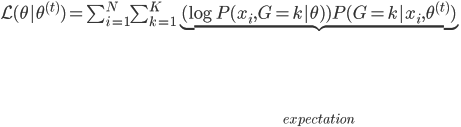 ,由于函数形式已知,我们可以计算并将
,由于函数形式已知,我们可以计算并将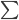 移出来,所以换成线性形式。
移出来,所以换成线性形式。
(3) M步:求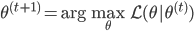 ,这样就完成了迭代。需要证明的性质是:随着迭代,
,这样就完成了迭代。需要证明的性质是:随着迭代,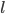 越来越大,且收敛。
越来越大,且收敛。
(4) 定理: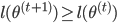 。
。
证明:

其中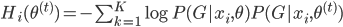 ,且
,且 ,定义为两分布的KL距离。
,定义为两分布的KL距离。
所以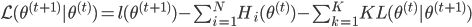 ,且
,且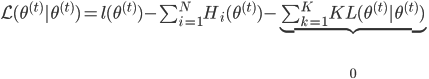 。而由M步,
。而由M步,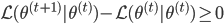 ,故有
,故有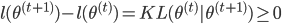 。
。
在GMM的情况下,应用EM算法,则有:
(1) E1步: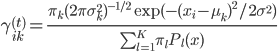 ,可以直接计算。
,可以直接计算。
(2) E2步: 。
。
(3) M步:注意有约束条件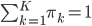 ,所以使用拉格朗日乘子法:
,所以使用拉格朗日乘子法:
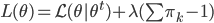 ,故有一阶条件:
,故有一阶条件: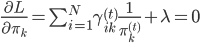 。从而
。从而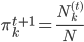 ,其中
,其中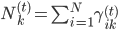 。
。
还有一阶条件: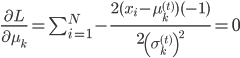 ,得到
,得到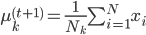 。
。
最后,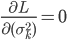 ,有
,有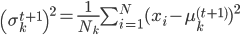 。
。
对GMM而言,E步和M步在k=2的时候,求解过程可参见书上。
第七章:模型评估与选择
1. 概念: 我们有数据集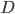 ,函数族
,函数族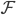 和损失函数
和损失函数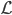 ,这样得到最优的
,这样得到最优的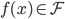 ,然后求得
,然后求得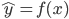
(有监督的学习)。之后就是对模型进行评估: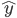 的精度如何(使用测试集)?模型的选择就是
的精度如何(使用测试集)?模型的选择就是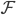 的选择,使得测试误差比较小。
的选择,使得测试误差比较小。
2. 方法:
(1) 数据充分:分成三块,1/2用来训练(train),1/4用来检验(validation),1/4用来测试(test)。其中validation
的概念是,在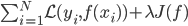 中,加入J函数来考虑函数族的复杂度,以避免过拟合。而validation就是来调正和选择这里的
中,加入J函数来考虑函数族的复杂度,以避免过拟合。而validation就是来调正和选择这里的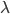 ,再用train和validation重新训练模型。
,再用train和validation重新训练模型。
最后,用test数据集,测试并且评估测试误差。
(2) 数据不充分:一种是cross-validation,分成k(比如5-10)份,极端的就是K=N,ave-win-out;另一种是bootstrap,后续章节详述。
4 replies on “≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记(十)”
加油做PDF
米有充足的时间 T_T
雇个秘书吧
唉,好高端的样子。