说说我所认识的“最小二乘君”（配图版）

由于近些年常常跟搞数据分析的人混迹在一起，所以很多时候说话方式有点偏向机器学习了...顺便心里暗暗的忧伤一下当年的心路历程（不知道我的基本轨迹的可以先去看看CV..）。这里聊作一二记录，讲讲我所认识的“最小二乘法”（下称最小二乘君）。那个，语言稍显浮夸，大家随便看看哈，别较真。

<锲子>

是写小说的时候大家都兴先来个“锲子”么。7年前，我还是一个年幼无知的大学新生儿。当时我们系开了两门传说中各挂50%的数学课：微积分和线性代数。同学们大都学的死去活来，我也学的死去活来，一度开始怀疑自己的智商...其实现在想想，我也不知道当年为什么学的那么痛苦，现在随手用个微积分貌似都很水到渠成的样子。嗯，可能是老师授课方式不够好吧。那年直到期末考试，我也不知道我学了一年的微积分有什么用处，除了背下来少数的几个证明推导和学会了一堆算微积分的“技巧”之外。

挂了很多人的高树...

线性代数也是一样的。当年翻看某本计算机类入门书（可能是算法与数据结构），前言一开始就是一行金字，大意是“矩阵论是当代计算机基础×××”。然后翻翻后面的果然看不懂，于是默默的去图书馆把这本书还了，然后借了一本黄皮的泛着金光《矩阵论》回来。同样悲催的，啥也没看懂，然后默默的放弃了我在这个领域深修的打算，乖乖的回去上必修课了。（所以我当年学习高级计算机知识的一腔热情就被这么无情的浇灭了哇！果断考完当时的计算机等级考试——C语言和数据库就扔掉编程了...）

线性代数一直学到最后，我还是以为这东西就是来替代“高斯消元法”解联立方程式的...什么特征根啊，奇异值分解啊，格拉姆－施密特正交化啊，直到最后我也没明白是干嘛用的，除了会算几个数之外...没想到，那日一别，重逢已是花落花开好几轮之后...当真是良辰美景虚设！只是万万没有想到，他乡遇旧友，而这厮竟和日后的最小二乘君紧密相连，难分难舍。

良辰美景虚设

第一回 未入宫门先试棋

大二的时候，我们系开始开专业课，夹杂在一堆××经济学里面稍稍偏数理的就是一门“计量经济学”了。听说讲课的老师也是数学背景，于是我们习惯性的心有戚戚焉。依稀记得那本经典蓝皮的南开张晓峒版《计量经济学基础》，第一节课的时候像圣经那样摆在我们每个人的课桌上。一开章，就是“一元线性回归模型”。第一次在书上见到了那么多弯弯曲曲的Σ，然后就是开始背一二三四五的“高斯马尔可夫定理”。嗯，那节课之后我们的课后作业是，手动计算20个x和y的回归系数估计量等...然后宿舍6个人居然按计算机加加减减都算出来五六个版本...最后大家一步步的检查...要知道一会儿Σxx，一会儿Σxy的，很容易出错哒！

摔！每个人算出来的都不一样！

自此开始最小二乘君在我小小的心灵中留下了一副高贵冷艳的形象，仿佛在说，“你们这些弱智的火星人还是快点回到太阳系去吧，地球上不适合你们生存”。后面开始讲置信区间...话说此时，“概率论和数理统计”上学期刚浑浑噩噩的学完，基本的概率论还搞明白，根本想不明白什么是置信区间...于是又背了几个公式飘过。后面讲基于线性回归结果的点预测，大家茫茫然听懂了，然后老师很无助的看着我们说，“那么区间预测就不讲了...”。那个，最小二乘君，您能再神秘一点吗？

最小二乘君：看到了么，失败者都在这里了，不怕死就来吧。

后面默默的开始学异方差，自相关，多重共线性三大恶魔，感觉自己就跟个初入门的医生似的，要各种对症下药。至于什么联立方程模型和两阶段最小二乘法，好吧我真的是又背了好多公式。这时候终于出现一点点和经济学相关的了！需求函数和供给函数！亲切的直想上去抱抱。然后默默的看到“联立方程模型的识别条件”君面色冰冷的挡在面前，只能默默的继续接招背公式了...

背公式 or 背咒语？

直到学完这门课，我也没想明白它到底跟我们同时在学的那些背一二三四五条的经济学课程有什么联系...也没想明白，为什么老师在某个我们埋头苦算的寂寞时刻，泱泱的说了一句“其实大样本下有了相合性（一致性，或consistency）之后，无偏性就不重要了）”...偶然飘入耳道的这句话被我们这些兢兢业业记笔记的孩子们默默的抄在了笔记本上，各种加粗、下划线、荧光标记来奉之为下一个“金纲玉律”，默默的期待有朝一日能亲自摸一摸这块闪着金光的牌匾...嗯，暂时不想了，默默的回去背大段大段的经济史了...

回想一下，貌似上学期最后一堂的“概率论与数理统计”课上，老师快速的讲完了方差分析，然后说，“下一章回归分析你们下学期计量经济学课讲的，我这里就不讲了”...导致我纳闷了很久，为啥这两章在这本袁荫棠的薄薄的桔黄色的小册子上是先后挨着的...这俩家伙到底有什么不为人知的关系？完全没看出来嗯...可见当年我是多么的乖巧。

（你能想象后面学过因果推断的我，是有多么想穿越时光回头扇扇当年那个不开窍的我..骚年啊，你怎么可以这么天真啊！）

叫你天真！

话说，这门课期末考试我创纪录的考了一个96（若干年来第一次看到这么高的分数...自打小学毕业之后就很少见了，以为大学都是及格万岁的），然后很开心的抱着成绩单安慰自己，嗯，你已经迈入数量经济学的门槛了。孰不知，此时还尚在门外徘徊，还没瞅见正道呢。

还有一件比较好玩的事儿，就是这一学期我们还开了一门“统计学”。一开始大家都以为是讲数理统计，然后就在第一节课的时候很狐疑的问老师，“这个跟我们上学期学过的数理统计有什么区别呢？”。老师慈祥而灿烂的一笑，“这门课我们讲的是经济统计。”何谓经济统计？基本上就是搜集经济数据的方法，好像还有编制经济指数之类。比如如何设计调查问卷！依稀记得那年的课堂作业是分组设计一个调查问卷（基本的原则就是不能诱导），然后找同学答卷（这里就是样本界定了），然后分析回收的答卷。事实证明，这么一门课对我后面研究生的时候理解实验设计那门课是非常有用的。因为经济学的田野实验对象都是人，所以它不是一门冰冷冷的学科，有的时候真的要靠一些技巧和智慧。工作之后，也明显的感觉到，当需要我设计问卷的时候，因为经历过这样的训练，思路很清晰...一步一步的怎么来，是用定量还是定性的回答，是文字还是选择题，如何投票排序之类。间接的也帮我在做采访的时候可以很快的列出来提纲...从我的理解，采访只是样本数N=1的时候调查特例嘛...哈哈。（默默的黑统计专业一下，居然很多学统计的都没有学过统计调查方法和实验设计，这里感觉至少在教学上经济学还是更胜一筹的）。

 统计学=下乡做田野调查

同年，值得记录的一个事件是，我彻底不去做网页前端的东西了。以前默默的写了很多的php, html, javascript那些代码，都老老实实的躺在硬盘某个角落开始沉睡了。我那时以为，那是自己和计算机的诀别吧。

第二回 层峦叠嶂雾重重

再一年，方才真正的被领进经济学的大门。看到辉煌的宫殿层层峦峦，各种大路朝天曲径通幽，一时开心的玩耍了起来。那年的经济学，仿佛被施了魔法似的，每一栋建筑顶上都挂着五颜六色的小星星，学习的过程仿佛就像是在打游戏通关，一个个小星星收入囊中。一年的时间，看着口袋里面的小星星慢慢多了起来，汇聚的光芒也愈发的强烈起来，不禁好开心。

一入宫门深似海

这一年，学完了“中级微观经济学”，才终于狠狠的复习了一遍忘得差不多的微积分。那时候，一种恐慌情绪在我们这些孩子中蔓延，因为有几位老师一直在说，“其实你们是没前途的。正儿八经的路应该是本科学数学，然后研究生转经济学，他们的数理基础比你们好太多...” 听完这样的话心里近乎绝望，开始疯狂的找各种机会学数学课。于是望向了另一边数学院那些乌黑冰冷的建筑群。除了本专业那些基本的数学之外，默默的去数学学院和金融数学专业或是旁听或是辅修的，开始被数学分析、复变函数、运筹学等等陌生的boss虐...依稀记得最后一学期不自量力的去修“泛函分析”的时候，外表慈祥的老师很无助的看着无知者无畏的我，说，“你来听听课我欢迎啊，你有问题来问就好了，想做作业助教也会帮你批，你为啥一定要拿这个学分呢？这个很难拿的呀！”...唉，事实证明，当年我的行为是有多么的在绝望中寻找希望，而世间本无捷径，想抄进路就要付出加倍的努力和承受额外的痛苦...

学完了中级微观，轮到了中级宏观。听说研究生的中级宏观是一位海龟老师上的，于是默默的跑到他班里去蹭课听。茫茫然的推导了很多公式，然后表示依旧对宏观不明觉厉...有意思的是，春季学期过去了，秋季学期同样的老师开的课是研究生的中级计量。当时已经大四，很多保研的孩子都会去蹭课，我也凑了个热闹去蹭。嗯，又要跟最小二乘君见面了呢。

咦，为嘛老师第一节课讲的就是“因果推断”？仗着反正我没选这门课得罪了老师你也拿我没办法的态度，回来就跟老师发邮件说，计量经济学怎么算是因果推断？充其量只是在黑屋子里面捉黑猫嘛！（这时候开始被统计之都毒害，别的没学会就学会讲段子了 -_-||）。来来回回几个回合之后，老师不理我了...呃，自作自受。然后默默的推导了一个学期公式，加结识了stata那个长得有点奇怪的生着绿眼眸的小黑孩儿之后，默默的投奔了出身名门望族的R君的怀抱。嗯，R君好有计算机编程的范儿，应该有这方面的血统吧？可怜那时候我还压根搞不清楚什么面向过程、面向对象、函数化编程这些东西...嗯，对的，09年我大无畏的跑到R会上凑热闹的时候，还完全没搞明白这些是什么...想想这些事儿已经过去4年了呢。

眨着碧绿眸子的Stata君

话说，那时中级计量的第二节课开始讲回归分析。嗯，我本以为自己已经见过最小二乘君了，这次可以潇洒的直接跟他打招呼了。咦，等等，怎么最小二乘君这里看起来有点陌生？咦，为什么他的长袍下面有矩阵君的印记？那个明明是矩阵君的记号！

最小二乘君二次现身

显然最小二乘君早已把我忘掉了。他开始随着老师在黑板上一行一行的写公式挥舞长袖，我赶紧一个字不落的开始抄笔记。然后回去看到作业，晕厥...晕厥几秒之后在一个又一个孤寂的自习的夜晚开始研究老师的讲义...一点一点的，我开始习惯带着矩阵君印记的最小二乘君。终究是变过了啊。

某节课，举手提问，老师说，“多重共线性在这里不重要啊，我们只关心它是不是一致的”。没明白，默默的抄在了笔记上，又一条金科玉律等待日后揭晓。

直到上完这门课，除了会推导plim了之外，完全没搞明白最小二乘君有什么用...还出来一个烦人的MLE君，在某些时刻下和最小二乘君形影相随，彼此替代...搞嘛搞啊，你俩啥关系啊...还有，那个为嘛时间序列那门课里面依稀也有最小二乘君的印记？好像，好像...

那时的感觉就是，仿佛学会了一门语言，却完全不知道可以在哪里用。

呵呵，果然都讲睡着了...

第三回 席地而坐谈风声

或许很多东西都需要时间的打磨，才能露出本来的色彩。后面开始读硕士，开始和一群受过很多年严格经济学训练的教授们学习。果不其然，一上来就是计量。大家应该都对瑞士人的守时有所耳闻吧，那么你能想象一个瑞士人教计量么？虽然我已经对带着矩阵君印记的最小二乘君变来变去的公式们习以为常，但是一个学期过后，还是要忍不住呼一声，“最小二乘君你以前有必要装的那么酷嘛？逼格那么高搞得大家都把你奉若神明似的有什么意思？”。然后最小二乘君腼腆的一笑，笑得我背后一身冷汗...“你还没见过随机试验君对吧，其实他也是我们家的，见过他你才算见过我们家族的第二位...”。

原来是你！马里奥你以前带着面具装什么酷嘛！

瑞士老师留给我印象最深的就是一个特别神奇的表格...倘若这个表格在国内学，那么八成就被我当成元素周期表横竖各背几遍应付考试了。因为瑞士老师前面一步步的讲明白了前因后果，带着我们一步步的推导和理解，所以最后我看这个表格的时候只能惊呼，“老师你为啥不早拿出来！”。对的，几乎不用去背，深深的印刻在脑海在里面。

好吧为了不吊大家胃口，我还是贴一下这个表格吧。那个，这个真的不是用来背的。另外，版权属于撰写讲义的Kurt Schmidheiny老师~我只是未经允许的copy&paste在这里...

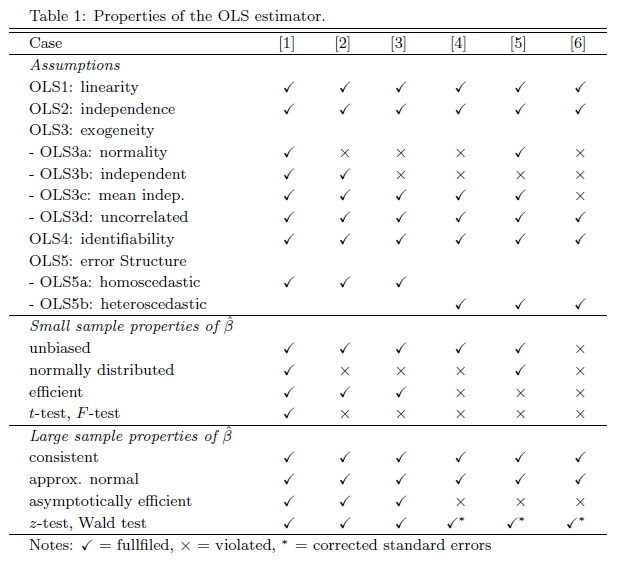至于每一条什么意思，我把图贴在最后面了，不跑题太远了...反正我假设你们是来看八卦而不是来跟我抢最小二乘君的。

嗯，后面陆陆续续的知道了最小二乘君更多的小秘密，尤其是在下一学期学过“实验设计”之后。与我来讲，随机分组只是一种策略，背后的道理只是为了保持可比性。于是在社会实验中，没法随机分配的时候，大家又有更多的补救策略。这里直接影响到的就是那年的硕士论文，因为我们试图在一个社会网络中通过田野实验的办法评估一个教育项目的价值。而后没想到的是，在工作之后一直在不停的参与实验设计、实验效果评估等等。那时打下的基础简直是救命...

跑题的说一件很好玩的事儿。怎么区别一个做网站数据分析的人是统计学还是计算机出身呢？来讨论一下评估方法吧！比如我们去看网站上一个广告的效果，那么计算机出身的人思路一般会偏向直接跟踪，比如一步步的看这个人的点击路径(基于cookie和session)，然后如果达成了某种认定的行为（比如下单购买），就认为是一个直接的成功案例；而统计学的会说，我们不去看某个具体的人的行为，因为有这些那些干扰因素，我们应该去把所有人一分为二，然后看实验组和对照组的表现差别。哈哈，每次听到类似的对话（或争吵），都觉得好有意思啊！各自有各自的信仰中的“golden rule”，嗯啊...

还是回到读书的年代。熬过了第一学期的密集数理训练之后，后面两个学期选了一些偏应用的课程。因为个人比较偏好微观计量（搞宏观计量的童鞋们，你们真的不担心过拟合么？！），所以选的课程偏劳动经济学，或者各种打着不同旗号比如发展经济学、教育经济学、卫生经济学、经济史的劳动经济学。因为这些实证的研究都是基于某些具体的现实问题的，所以突然间觉得最小二乘君格外威武。虽然大家现在会更倾向于GMM那些方法，但是几乎每个人在汇报结果的第一列都是最小二乘君的结果。baseline。简洁优雅的最小二乘君仿佛就是做手术的时候，解剖外皮的第一把利刃，然后我们用更精细的其他工具来探究更具体的问题。直到此时，方才觉得，无论是最小二乘君还是他家族里面的其他高富帅白富美们，流淌着传承着的都正是统计的血液。统计学是一种思想（和某些时刻做出判断的准则），无论是发展到计量经济学那样专情于因果推断，还是延伸到统计学习那样关注预测效果，其实给出的都是用数据解决具体问题的思路（i.e. 现在有一个现实的问题，有一些数据或者还没有，你能告诉我怎么可以一步步作出有意义的判断么？）...如果只沉浸于某些具体的模型，反而有点得不偿失了呢...（这也是最近yihui开始批判我，偷懒不写小册子的理由居然是那些不重要...“尼玛你觉得不重要不代表对入门者不重要啊？你自己走过的坎坷之路你就不帮帮后来者啊？” 我错了...可是真的，我还没想好怎么讲这条坎坷的道路，先借这里讲点八卦大家开心一下好了）。

话说，这期间落下的一个不良的习惯就是，往后面试最喜欢考统计学孩子们，“你推导一下最小二乘估计量吧”“你说说高斯马尔可夫定理每一条都是什么意思吧！”，然后脑子里面默默回想当年那个神奇的表格...基本功啊基本功。

第四回 落花时节又逢君

刚开始工作的时候，偶尔就是调戏一下最小二乘君，做做简单的随机试验什么的。与此同时，开始接触“协同过滤”那些东西。依稀记得那年老板直接扔给我几篇论文，说“你看看这个就理解我们做什么的了...”。果不其然，我看懂了公式，却没看懂背后的逻辑。协同过滤到底是什么路数的哇！

在那几年，“推荐系统”仿佛成为了一个吸引投资的金字招牌，夸张到当时我和朋友在复旦后面那条街的某个小饭馆吃饭，然后等餐的时候就听到旁边那桌在讨论推荐系统...顿时真想摔盘子走人哇！后面又开始炒作“大数据”概念，然后发现各种大数据会议上推荐系统永远是一个永恒的话题...搞计算机的在搞推荐系统，搞物理的搞复杂网络的在搞推荐系统，搞统计的在搞推荐系统...除了协同过滤，大家还在研究各种各样的预测模型，搜集各种各样的数据，试图打通消费者行为的各个环节...比较夸张而也是听起来也挺靠谱的主意就是，利用推荐系统来给使用数据仓库的分析师们计算是不是改赋予各种表的权限...咳咳。

摔！

反正一个东西浸淫久了，总会多多少少了解一些内幕。那年我虽然是几乎不写程序的（主要负责跟人打交道，不是跟电脑打交道），但是为了更好地理解业务我也百无聊赖的去看了一些协同过滤的原理之类。哎，不就是一个矩阵转来转去嘛...

后面换工作了，开始悲催的码代码了，然后开始去复旦蹭课了，才有机会从头开始学一遍统计学习（或曰机器学习）这些东西。当时蛮诧异的看着老师在讲ESL的时候前几节课也是在推导最小二乘君，只是用的是另外一种思路来解释：测试误差最小（计量其实不是很关心这个...），也第一次接触到训练误差和测试误差这种评价思路。而后看到带正则项的岭回归或者Lasso，自然而然的先去攻击一下，“你们俩是一致估计么？”，随后看到一群鄙夷的眼神，“我们不关心估计量是不是一致的，我们关心的是减小测试误差”。呜呼哀哉，原来最小二乘君在计量经济学之外也有这么多人爱戴着...原来他还可以这样出现在我面前...

呵呵，你以为朕就属于你一个人么？太天真了！

复旦的ESL偏向理论，基本上是一个学期内推导了一下各种各样的模型。秉承着抄好笔记回家慢慢理解的原则，板板正正的笔记顺便复制到了落园上（实际是我在LYX里面辛辛苦苦一个一个字码出来的...）。后面Coursera开课了，就去兴高采烈的选了Andrew Ng的机器学习，兢兢业业的跟着作业码了一学期。嗯，果然是计算机出身的，更涉及到实现。比如我原来一直不理解，为什么RHadoop里面（rmr2包），最小二乘法的实现是通过并行重抽样实现的，以前满脑子里面都是我最喜欢用来面试的“解析解”——X'Y/(X'X)！以为并行的根基就是解决矩阵乘法的并行计算问题。后面学到各种数值解的方法，才恍然大悟，原来这个是可以迭代来解的！原来这个是可以借助大数定理和中心极限定理通过重抽样来算的！而这些想法自然而然的都可以通过并行来解决...哎呀呀。瞬间感觉我以前是太小看最小二乘君了，too simple sometimes naïve。以前总觉得统计模型那块推导还是偏数学的想法，一步步的来证明嘛，后面才发现真正实现的时候借助的才是统计学的思路，抽样抽样抽样！什么蒙特卡洛方法，不是仅仅在帮助证明某个估计量的分布的时候才有用的（以前学计量的时候只在这里用到过），而重抽样的思想完全适用于数值解..哎，明明就是一层薄薄的窗户纸，以前我咋就没想明白呢...

后面看到COS上的一篇八卦，

Rafael Irizarry教他上五年级的儿子用最小二乘法改进机器人模型，最小二乘是统计学家的看家本领，普通得不能再普通，但在Rafa手里用出来却让人不得不佩服。

方才直观的理解为什么机器学习又和人工智能（AI）走的那么近...我发现我只有看到现实的案例，才会突然间恍然大悟以前学过的那些书本知识有嘛用...所以是，“学而不思则罔，学而不用则die么”...

天真的人类啊，你难道不知道你们只是上帝我创造的一些玩具？啊哈哈哈...

好吧，最小二乘君，直到今日，我方才理解为什么高斯君当年那么兴奋...哎，我怎么就没有在一开始就看到你的诸多光辉，而白白浪费了我们相处那么多年的美好时光呢？

-------------------暂时没有了，不时想到更好玩的再补上----------------

<番外I >

OLS的假设们，配合第三回神奇表格一起看。