高阶的曼妙

最近业余看了一点抽象代数，本以为会根本看不下去，结果没想到抽象代数居然如此好玩。看过了抽象代数，再去看很多东西，仿佛就是降维打击，轻巧曼妙。

环（ring），域（field），群（group），三个相辅相成的抽象概念，笼络了常见的各种代数运算（加减乘除和矩阵运算）和代数定义域（整数，有理数，实数，复数），居然就这么轻轻巧巧地被串起来了。最有意思的是，这一系列对于代数结构的理解，使得“一元高阶多项式有没有一般解”这个问题得到了彻底的解决，让人拍案叫绝。

有意思的是，我最近发觉自己对于英文的理解能力比中文略强，尤其是在数学这块儿，所以我就先去看的英文课程（也有可能是教学风格不同，西方的老师有一种绞尽脑汁深入浅出地倾向）。写这篇日志的时候，翻了翻中文资料，发现豆瓣的一篇帖子讲得非常好，但是豆瓣不显示公式，于是有人很贴心地提供了latex排版并放在GitHub上。我看的英文课程是从环，域，群这三个概念开始讲的，到最后才提供了“五次及以上多项式没有根式解”作为一个实例，让人看得特别有满足感。

抄一下最核心的证明思路：

这样伽罗华（Galois）证明了：一元n次多项式方程能用根式求解的一个充分必要条件是该方程的伽罗华群为可解群。

由于高于四次的一般方程的伽罗华群不是可解群，也就直接推论出高于四次的一般方程的不可解性。

也即伽罗华发现本质就是：域的无数种扩张方式其实就是有限阶的群。n阶对称群对应着n次一元方程，而5阶和5阶以上的对称群不是可解群，也就是五次和五次以上的代数方程没有求根公式。

如果回顾历史，会发现在Galois之前的数学大家，如拉格朗日，解决问题的思路都是降维：试图把高阶方程变化为更低阶的问题。如果每个n阶都可以简化为n-1阶的问题，那么所有n阶方程的解不久解决了吗？结果拉格朗日就被卡在这样的归纳法思路了。

Galois另辟蹊径的地方在于他没有沿用这种简单的归纳法的思路，而是回到了代数的本质。这么想，

• 人们为了得到一次方程的一般解，需要拓展整数数域，引入有理数。即 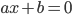的通用解 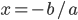并不是在整数域之内，而是要引入有理数。
• 人们为了解决二次方程，又不得不拓展有理数，引入了根式，从而引入了无理数和复数。二次方程的通用解里面必须包括根式，而当 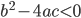的时候，就不得不引入复数了。
• 三次方程简化后的辅助方程为二次，四次方程的辅助方程为三次，所以暂时不需要引入新的数域。
• 五次及以上方程就没这么幸运了， 由于其对应的伽罗华群不是可解群，所以在复数范围内是没有一般解的。

这里有一个很有意思的问题，为什么到五次方程，事情就产生了质变呢？Galois给出了事情的本质：五次及以上的多项式方程不存在在根式定义下的可解群。

可解群本身的定义依赖于正规子群、极大正规子群列及确定极大正规子群列的一系列合成因子。Galois定义了，如果一个群所生成的全部合成因子都是素数，则称这个群为可解的。所以，如果不拓展根式数域，五次及以上方程就没办法变成可解群了。换言之，不是五次及以上方程无一般解，而是加减乘除和根式运算限制了我们对一般解的表达能力。

这里可以看出为什么抽象代数为称之为抽象代数了，因为到这里，对于代数的理解就不仅仅是满足计算目的了， 而是去理解代数本身的结构。素数作为整数域里面的基本元素，不仅仅影响着因式分解，还可以拓展到整个代数结构里面去。某种意义上，我们需要在抽象代数里面重新定义“素数”或者基本元素，然后便有了各种优美的结论。

我在可见的未来之内，估计是不会亲自用到抽象代数了。只是这种思维的曼妙和在（更）抽象层面上洞悉事物本质的爽快感，让人着实欲罢不能。

---

最后补一句最近的人生感慨。很多时候，我们觉得一个（局部）问题很棘手无法解决，很可能是我们手上的工具限制了我们解决问题的能力。这个时候需要做的不是死磕，而是重新定义问题，从一个更高的层面来看待这个问题，或许就会看到自己曾经的局限性。定义问题永远比解决问题更重要。