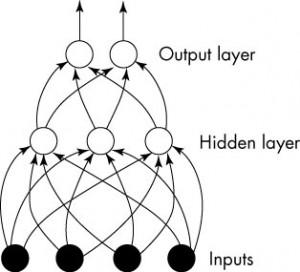
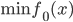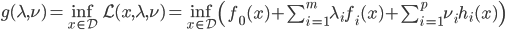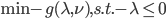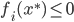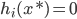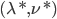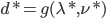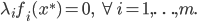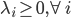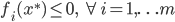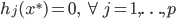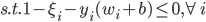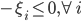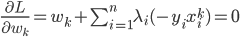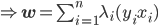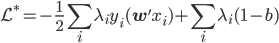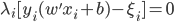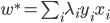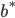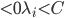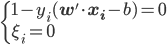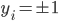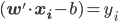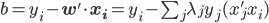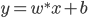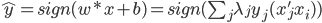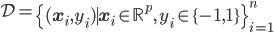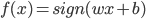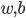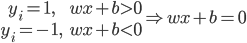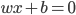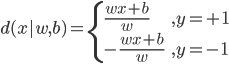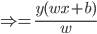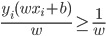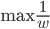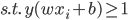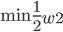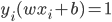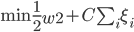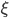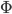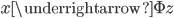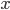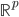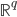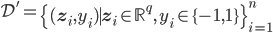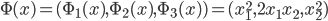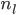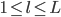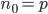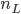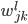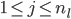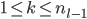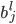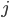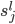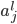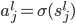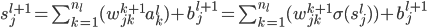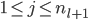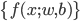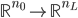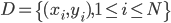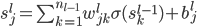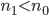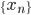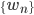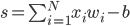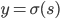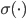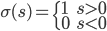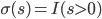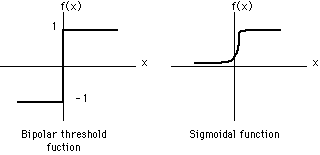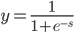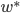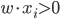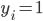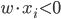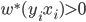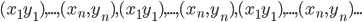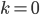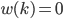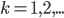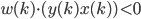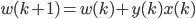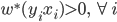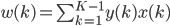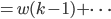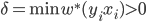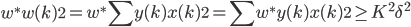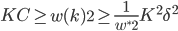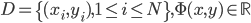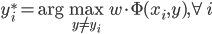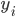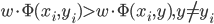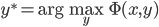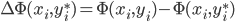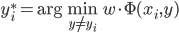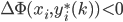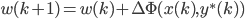神经网络,这是要开始Deep Learning了么?
神经网络的历史和大起大落还是可以八卦一下的...
第一波:人工神经网络起源于上世纪40年代,到今天已经70年历史了。第一个神经元模型是1943年McCulloch和Pitts提出的,称为thresholdlogic,它可以实现一些逻辑运算的功能。自此以后,神经网络的研究分化为两个方向,一个专注于生物信息处理的过程,称为生物神经网络;一个专注于工程应用,称为人工神经网络。
第二波:上世纪80年代神经网络的研究热潮。带反馈的神经网络开始兴起,其中以Stephen Grossberg和John Hopfield的工作最具代表性。很多复杂的认知现象比如联想记忆都可以用反馈神经网络进行模拟和解释。一位在神经网络领域非常资深的学者跟我聊天时说,在那个年代,只要你的文章跟神经网络扯上点关系,无论什么杂志,都很容易发表。
第三波:直到2006年深度网络(deep network)和深度学习(deep learning)概念的提出,神经网络又开始焕发一轮新的生命。深度网络,从字面上理解就是深层次的神经网络。至于为什么不沿用以前的术语“多层神经网络”,个人猜测可能是为了与以前的神经网络相区分,表示这是一个新的概念。这个名词由多伦多大学的GeoffHinton研究组于2006年创造。事实上,Hinton研究组提出的这个深度网络从结构上讲与传统的多层感知机没有什么不同,并且在做有监督学习时算法也是一样的。唯一的不同是这个网络在做有监督学习前要先做非监督学习,然后将非监督学习学到的权值当作有监督学习的初值进行训练。
上述来自:http://www.caai.cn/contents/118/1934.html
有没有感觉最近deep learning热得一塌糊涂?好像是个人都知道有这么个词儿但是真正知道他干什么的、怎么来的的人却不怎么多。嗯,貌似从这节课开始,要掀起deep
learning的篇章咯。顿时感觉好洋气哇。
----------正文的分割线-----------
这节课先介绍七十多年前的Perceptron模型。
1. 神经元
大致就是这样一张图片。神经元细胞有个大大的细胞核,然后有个轴突。如果神经元细胞拼在一起,可以构成一个神经网络。
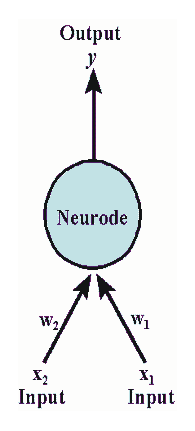
(我觉得这个细胞模型和后面的东西其实没太直接的联系...就是一个很好看的图...)
2. Perceptron模型
Perceptron模型有若干输入: ,标记为
,标记为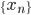 序列。
序列。
每个输入都有一个权重(某种程度上可以理解为信息损失): ,标记为
,标记为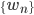 序列。
序列。
最后每个“细胞”还有一个偏(门限):b,即我们常说的常数项截距。
最终的状态: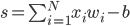
输出: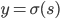 ,比较简单的情况下,
,比较简单的情况下,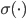 可以是一个二元输出函数,比如
可以是一个二元输出函数,比如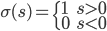 或者写作
或者写作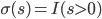 。但是比较讨厌的是这个函数不可微,所以我们可以转成一个可微的函数(有点类似logistic regression的思路,用概率的密度函数来做)。
。但是比较讨厌的是这个函数不可微,所以我们可以转成一个可微的函数(有点类似logistic regression的思路,用概率的密度函数来做)。
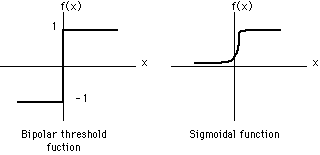
可微的情况下,这个输出就是: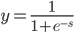 ,这样就可以做成一个光滑的曲线了。
,这样就可以做成一个光滑的曲线了。
3. Perceptron算法
给定一批数据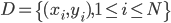 , 我们希望求得
, 我们希望求得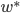 使得
使得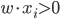 ,如果
,如果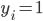 ;否则,
;否则,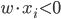 (即
(即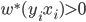 。
。
算法:先是我们可以不断重复的无限复制数据: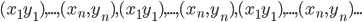
然后初始化: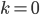 ,
,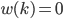 。
。
开始循环:
For 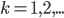
IF 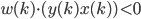 ,then
,then 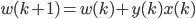
定理 如果存在w使得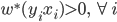 成立(即平面线性可分),则Perceptron算法在有限步收敛。
成立(即平面线性可分),则Perceptron算法在有限步收敛。
证明:
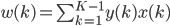 (仅计算改过的)
(仅计算改过的)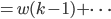
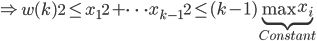 。
。- 存在
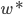 使得
使得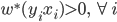 ,那么我们有
,那么我们有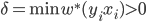 ,
,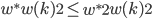 ,同时我们有
,同时我们有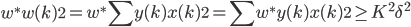 这样就会有
这样就会有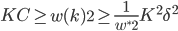 ,当k趋近无穷大的时候,显然左式不成立。所以必有在某个k的时候停止迭代。
,当k趋近无穷大的时候,显然左式不成立。所以必有在某个k的时候停止迭代。
4. 推广至多类——Collins算法(2002)
(1) Collins表述
给定 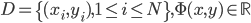 ,求w使得
,求w使得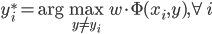 ,除了
,除了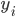 外最大。这样
外最大。这样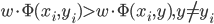 。
。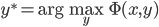 。
。
(2)算法: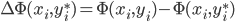 ,
,
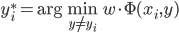 。
。
初始化: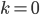 ,
,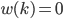 .
.
For 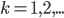
计算 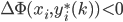 ,
,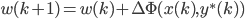
输出: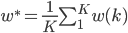
(3)定理。若为线性平面可分,则在有限步内收敛。
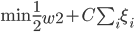
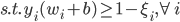
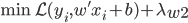
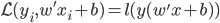 。
。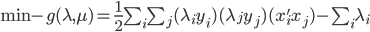
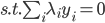
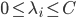
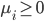
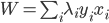
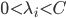 ,
,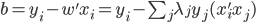 ,然后
,然后 。
。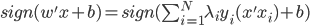
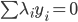 的约束),之后就可以解这个双变量优化问题。
的约束),之后就可以解这个双变量优化问题。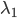 ,
,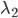 作为变量,其他
作为变量,其他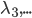 作为常量。
作为常量。
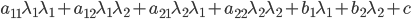
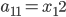 ,
,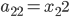 ,
,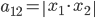 ,
,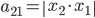 。
。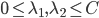 (对应对偶问题)
(对应对偶问题)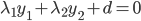 ,这里d代表其余不改变的那些
,这里d代表其余不改变的那些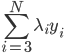 。
。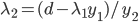
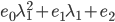 ,最优条件
,最优条件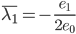
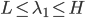 ,其中
,其中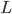 和
和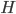 分别为lower/upper bound。故必有最优点在L、H之间或者L、H之一。
分别为lower/upper bound。故必有最优点在L、H之间或者L、H之一。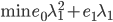 ,
,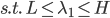 ,可以解得
,可以解得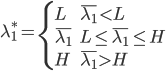
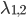 ,第一个变量
,第一个变量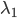 可以选择
可以选择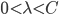 ,同时
,同时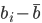 最大。第二个变量选择
最大。第二个变量选择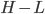 最大的。
最大的。