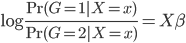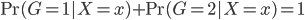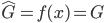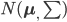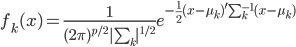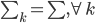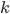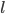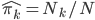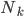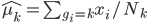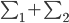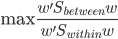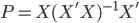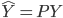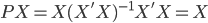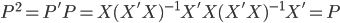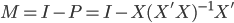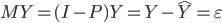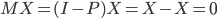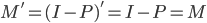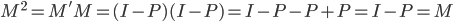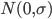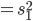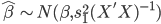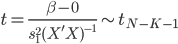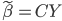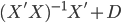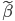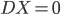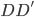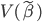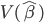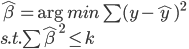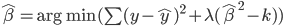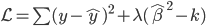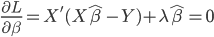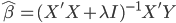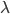昨晚看到一篇广为流传的房奴文章,比如网易上转载的,实在是让我忍无可忍,决定抄起笔来对付一下这种用数字挑逗民意的行为。真受不了~~~
首先这类文章都会有一个很鲜亮的标题,比如这里的“三代房奴面面观:一代赚满 80后才是真正房奴”。房奴,80后,这两个词加起来就够吸引眼球了,还有“三代”,真的是三代通杀。其实我也没资格批评别人,前段时间写个SAS笔记还搞个“七天搞定SAS”这种噱头,明显动机不纯。
不过题目吸引人也就罢了,正文读下来八成要让人义愤填膺一番。感觉自从今年春天借给松鼠会做讲座的机会,看了一眼现在的新闻之后,就对各种挑逗的方法有了更强的免疫力。
挑逗民意最最典型手段就是以“个例”代替群体。这句话怎么说呢,其实就是不断的举出各种极端的例子。比如这篇文章,对于三代人,各找了一个代表:
70后:于先生
-年龄:35岁
-职业:某金融行业公司品牌策划室经理
-房产:南三环外丰台西马厂区域两居
-2007年购买时单价:6500元/平方米
-2012年该项目二手房单价:约29000元/平方米
35岁的于先生说,目前为止,自己还是一名房奴,但相比2007年买房那会儿,已经轻松和洒脱多了。
80后:陈女士
-年龄:31岁
-职业:广告公关公司合伙人
-房产:东城区富贵园
-2006年购买时单价:10000元/平方米
-2012年该项目二手房单价:38000元/平方米
我就看不大明白了,明明两个人才差了4岁,购房也只差了1年,怎么就被归为两代人的代表了?两个人的故事也没什么大的差别嘛,房价都翻了三四翻的样子。这两个其实还好,最让我看不下去的就是最后一个90后的例子:
90后房奴:生活乐趣才是王道
-人物:赵悦
-年龄:22岁
-职业:资产管理公司销售
-房产:朝阳区小悦城
-2012年4月购买时单价:37000元/平方米
-2012年该项目二手房单价:38000元/平方米
将90后这一代称作房奴可能并不准确,他们中的大多数人刚刚念完大学,但已有不少人也挤进了买房大军。但相对于80后的不堪重负,90后房奴更加轻松,从来就没觉得这是他自己需要承担的。
赵悦是一个重庆姑娘,2011年在英国念完书便来到了北京,父亲是重庆一家国有企业的老总,靠着父亲的关系,她很容易就在北京一家资产管理公司找了一份工作,每月薪酬将近8000元。
赵悦告诉记者,回国没几个月,家里就掏钱给她在朝阳的小悦城买了一个小公寓。这个楼盘位于朝青路上,距离年轻人扎堆的大悦城只有800米,那里聚集着优衣库、H&M等潮店,还有天天人满为患的各种麻辣香锅。“买这房子主要还是因为公寓不限购,而且一个人住也够了。”
赵悦选中商住两用的公寓不在限购范围之内。按照当时的房价,40平米的loft,单价38000元左右,一套房子150多万,不过这样的产权只有40年。“我其实对房子并没有感觉,从来也没觉得回国之后就要买房子,是父母觉得应该有个固定的房子。”
家里为她付了8成首付,只是象征性地贷了一点款,这是因为父母不希望赵悦花钱“月月光”。现在,赵悦每个月要还2000多块钱房贷,这一还款额在北京这样一个城市并不高。但即便是这样,赵悦还是觉得钱不够花。看看赵悦的生活账单,几乎80%钱用在了娱乐消费上,而她自己永远都不太清楚钱到底花到哪里去了。
由于小悦城还没有交房,赵悦在离金融街不远的官园租了一套精装一居室,房租5000元。这里几乎成了金融街的后花园,聚集了大量在金融街上班的小白领。如果全靠赵悦的工资,8000的工资交完房贷、房租,就剩下不到1000了,这点钱还不够她打车的。
赵悦父亲对她比较严厉,但她母亲则更宠爱她,直接给她交了一年的房租,即便这样,赵悦还是寅吃卯粮,经常刷爆信用卡,母亲经常替她还款,还时不时地暗中接济她一些零花钱。
对于国人热衷的房子,赵悦觉得有些不可思议。她自己数了一下,父母的房子、爷爷奶奶的房子加上购买的小公寓,在北京、重庆总计有六套房子。“我都不明白还不够么,我没法理解大家为什么这么热衷于买房子。然后把所有的钱都用来还月供,而每天的日子都过得惨兮兮。”
看看这些数字: 月收入8000(不算低),房租5000,贷款首付80%...一个个都是让人瞠目结舌的数字。通篇下来,90后被描述成了一个彻头彻尾的啃老族和富二代。可是,我们都知道,举例是最常用的论述方法,可是也不能总找最极端的例子吧?田忌赛马的道理大家都知道,总不能拿最差的和最好的比吧?
只是想问几个问题: 70、80后就没有月光和啃老族了么?70、80后在20出头的时候(现在90后的年纪)就不会寅吃卯粮么?拿70后的经理和80后的合伙人,跟一个90后的小销售比,这样公平么?
好好的文章,就从来不能保持客观。相比而言,有时候我觉得CCTV的新闻采访靠谱多了...纵是这样大家都在不停的咒骂。哎,新闻什么时候能保持中立性呢?