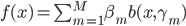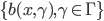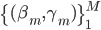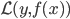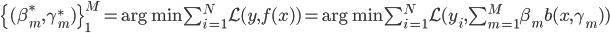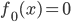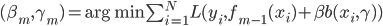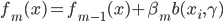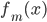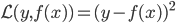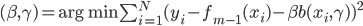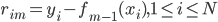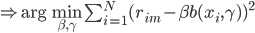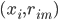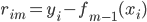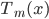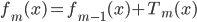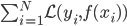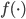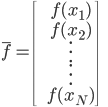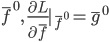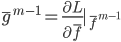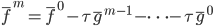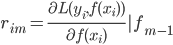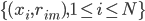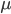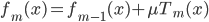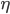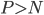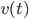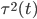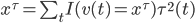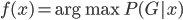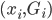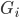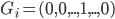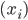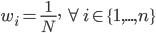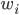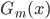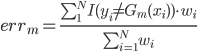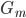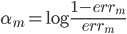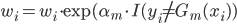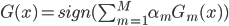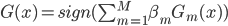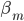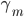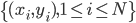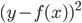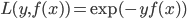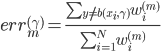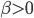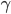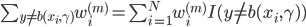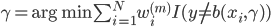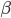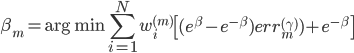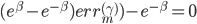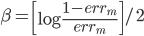第十五章 随机森林(Random Forest)
终于讲到这个神奇的算法了...若是百年前的算命术士们知道有此等高深之术,怕是要写成一本《随机真经》作为武林宝典世代相传了吧?猜得准才是王道嘛。
p.s. 以前没看过的童鞋不要急,这节课只是从boosting直接跳讲到十五章,并不是已经快结课啦。
---------------
1.定义和算法
算法:
- 1. For b = 1 to B
- 生成一个自生样本
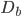 (via bootstrap)
(via bootstrap) - 由
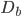 生成树
生成树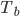 :
:
- 随机选取m(
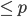 )个变量(相应的
)个变量(相应的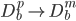 ,取了m维子集)。一切的神奇都在于这里是随机降维的。
,取了m维子集)。一切的神奇都在于这里是随机降维的。 - 由
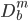 生成树
生成树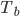 。
。
- 随机选取m(
- 生成一个自生样本
- 输出
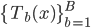 (即森林)。
(即森林)。
随机森林算法的参数主要就是决策树的参数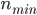 ,用来控制树的生长的:保证每个叶子中的实例数不大于
,用来控制树的生长的:保证每个叶子中的实例数不大于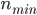 。
。
应用
1) 回归 在回归的情况下采取均值,最终输出的就是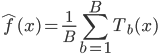 .
.
2) 分类 分类的情况下进行投票, ,得票最多的那类获胜。
,得票最多的那类获胜。
参数
总结的来看,参数主要有如下几个:
- B:试验次数。一般为几百到几千,所以是computational intensive.
- m:降维的力度。作者建议回归的情况下采用
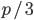 ,然后分类的情况下采用
,然后分类的情况下采用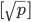 。
。 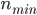 :建议回归的时候设为5,分类的时候设为1(彻底分到底)
:建议回归的时候设为5,分类的时候设为1(彻底分到底)
伪代码
其实上面已经写的比较清楚了...我只是再抄个伪代码过来而已。
select m variables at random out of the M variables
For j = 1 .. m
If j'th attribute is categorical
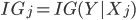 (see Information Gain)
(see Information Gain)
Else (j'th attribute is real-valued)
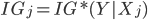 (see Information Gain)
(see Information Gain)
Let 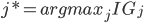 (this is the splitting attribute we'll
(this is the splitting attribute we'll
use)
If j{*} is categorical then
For each value v of the j'th attribute
Let 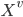 = subset of rows of X in which
= subset of rows of X in which 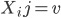 . Let
. Let 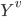
= corresponding subset of Y
Let 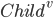 = LearnUnprunedTree
= LearnUnprunedTree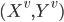
Return a decision tree node, splitting on j'th attribute. The number
of children equals the number of values of the j'th attribute, and
the v'th child is Childv
Else j{*} is real-valued and let t be the best split threshold
Let 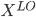 = subset of rows of X in which
= subset of rows of X in which 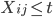 . Let
. Let
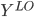 = corresponding subset of Y
= corresponding subset of Y
Let 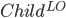 = LearnUnprunedTree
= LearnUnprunedTree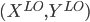
Let 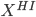 = subset of rows of X in which
= subset of rows of X in which 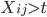 . Let
. Let 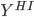 =
=
corresponding subset of Y
Let 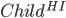 = LearnUnprunedTree
= LearnUnprunedTree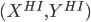
Return a decision tree node, splitting on j'th attribute. It has two
children corresponding to whether the j'th attribute is above or below
the given threshold.
2. 为什么要“随机”
bootstrap:通过多次重抽样减小误差。
考虑下面的情况:
1) 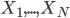 为随机变量,且
为随机变量,且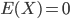 ,
,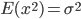 。
。
(i)当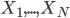 相互独立的时候,
相互独立的时候,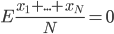 ,且
,且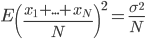 。
。
(ii)当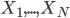 相互不独立的时候,我们有
相互不独立的时候,我们有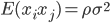 。这样接下来就有
。这样接下来就有
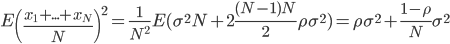
如斯,仅使用bootstrap的话压缩的是方差的第二部分,而随机选的的M可以减小样本之间的相关性,从而减少不同树之间的相关性。
2)OOB(out of bag)实例
OOB的概率: 。这样就是说,在一次抽样中约有1/3的样本没有被抽到。
。这样就是说,在一次抽样中约有1/3的样本没有被抽到。
两次bootstrap抽样的话,样本约有40%的重叠,这样的重叠概率会影响到上面的(ii)中,两次抽样得到的样本重叠很高,相互不独立。
这样我们用67%的样本训练数据,用剩下33%来测试。
3. 其他应用
1)变量的重要性(feature selection,俗称的特征选择)
第一种方法可以和上节课梯度树那里的一样,用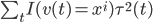 来刻画变量的重要性。
来刻画变量的重要性。
第二种方法则是比较有意思。对于一棵树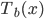 ,我们用OOB样本可以得到测试误差1。
,我们用OOB样本可以得到测试误差1。
OOB样本大概长成这个样子:
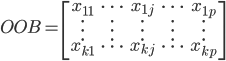 ,样本量足够大的情况下
,样本量足够大的情况下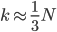 。
。
然后随机改变OOB样本的第j列:保持其他列不变,对第j列进行随机的上下置换,得到误差2。至此,我们可以用误差1-误差2来刻画变量j的重要性。当然这里loss function可以自己定。这里的大致思想就是,如果一个变量j足够重要,那么改变它会极大的增加测试误差;反之,如果改变它测试误差没有增大,则说明该变量不是那么的重要。(典型的实用主义啊!管用才是真,才不管他什么证明不证明呢!自从开始接触机器学习的这些算法,我真的是被他们的各种天真烂漫的想法打败的一塌糊涂,只要直觉上过得去、实际效果看起来比较好就可以了呢,规则真简单)。
2) 相似图(proximity plots)
除了用户变量选择之外,Random Forest也可以给出各个观测实例之间的相似度。
Proximity plots记作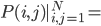 在一个叶子结点
在一个叶子结点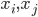 同时出现的次数,其实大致就是一个相关性矩阵的样子。思想其实就是,如果两个观测样本之间比较相关,他们在树分枝的过程中就比较难以分开,所以会经常一起出现。我们故而可以用一起出现的次数给这种相似程度打分。
同时出现的次数,其实大致就是一个相关性矩阵的样子。思想其实就是,如果两个观测样本之间比较相关,他们在树分枝的过程中就比较难以分开,所以会经常一起出现。我们故而可以用一起出现的次数给这种相似程度打分。
树类算法
至此,我们大概一口气过掉了所有跟树相关的算法。
先是单一的决策树,然后是基于已有弱分类器的改良算法,比如梯度树,然后就是和梯度树不相伯仲的随机森林。我感觉随机森林真的是起了一个好名字,在我没学机器学习之前就听到无数人跟我说起随机森林,而梯度树却只是正儿八经开始看了才记住的名字...
下下周开始,会依次讲到神经网络和SVM...看来supervised learning就快拉上帷幕咯。