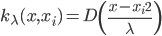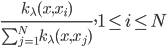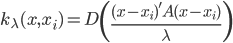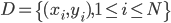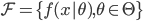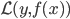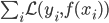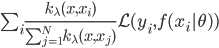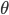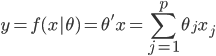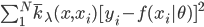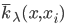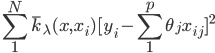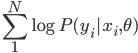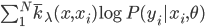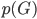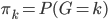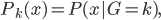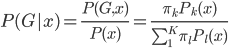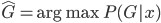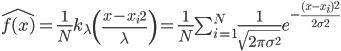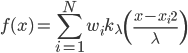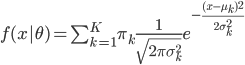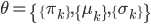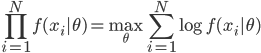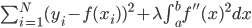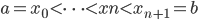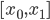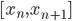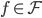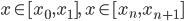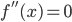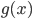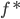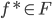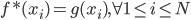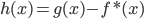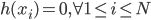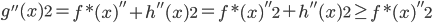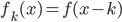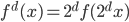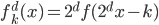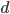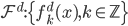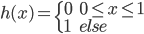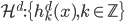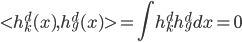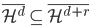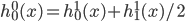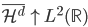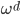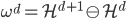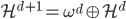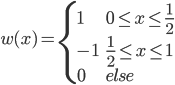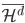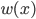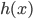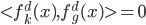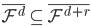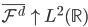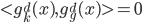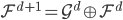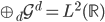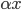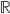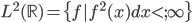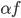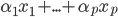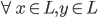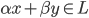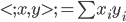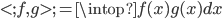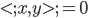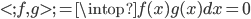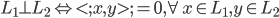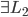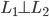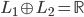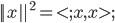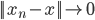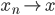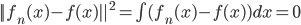有些东西,长时间不看不推导,难免就忘了。最近感觉不断的有人来问类似的问题,基本都是集中在实验设计阶段的(貌似很多时候学校里都不教大家怎么设计实验?只有设计好了才知道怎么评估嘛...)。索性趁着有点时间,复习一下计量经济学对付实验的一些方法。
其实已经不知道第多少次在落园说到社会实验的问题了,不过貌似都未曾从零开始系统的讲述过(其实有的时候基础的问题才是最大的问题)。还是乖乖的拿起「Mostly Harmless Econometrics」这本书和当年的笔记,乖乖的重新当一回虔诚的学徒...这本书是经济学家写的,所以例子大多是经典的经济学尤其是劳动经济学(Labor Economics)的例子。我会替换掉一些学术性比较强的例子,但是也会损失一些严格性,以保持直觉为第一要务。大家还请酌情依据自己的知识积累来有选择的吸收。

Mostly Harmless Econometrics
本文主要以读书笔记形式为主,但是会非常多的加入我个人的一些观点和点评。原文翻译部分会以引用形式标出。此外,发现读者们越来越喜欢“短平快”的东西了,我也只能试图把文字写的更加的深入浅出一点,笑点多一点...
p.s. 刚看到《机器学习那些事》这篇译文,想稍稍补充一下。计量经济学关注的不是预测,而是(统计上的)“因果推断”。所以衡量的标准什么的自然也有所不同,还请不要以预测的标准来看待下文。
-----------絮叨结束,笔记开始-----------
实证研究的四个FAQs
(废话一句,前段时间整理了一堆统计应用的问题,可惜现在不能发啊不能发,等答案来了一起发吧...) 做research的,大多会被四个问题所困扰:
1. 探究哪种程度的关系?
2. 理想的实验怎么设计?
3. 最佳的识别策略是什么?
4. 结果怎么解读?
这四个问题基本就是一项实证研究的四个步骤,找到一个自己感兴趣的问题,然后去找出一条路子回答它,再择选最优的数据分析策略,最后从数据回到直觉,来解读这些结果。这样,基本上从「直觉 -> 数据 -> 直觉」,一气呵成。前两天施老师一直在微博上感慨:
我觉的目前中国最奇缺的也不是数据分析师,也不是创造商业价值的想法。我觉得最缺的是独立思考和用事实与数据支持并表述自己想法的习惯和能力。
有点不谋而合的感觉。独立思考(直觉) -> 事实与数据 (数据) -> 支持并表述自己想法(直觉)。许多次,我在面试中被问及“为什么去学习那么多统计模型或者更直接的、为什么喜欢和数字打交道”的时候,总会说一句:
从数字中寻找直觉。
这句话从凯恩斯那里抄过来之后,一直被我奉若圭臬,不时拿出来提点自己一下也不错。说到底,我有点不是很喜欢数量分析模型的滥用,虽然现在已然是普遍现象...
一个一个来看。
第一个问题:为什么强调(统计上的)因果关系而不仅仅是相关关系?
无数次的回答过这个问题,尤其是在今年春天两次讲「别让数字吓到你」的时候...反例说过很多了,关键在于,我们一般观察到的相关性,为什么不能直接用于“政策设计”上的指导呢?套用一句经典的中文,相关性就是「知其然、而不知其所以然」。因此,大多数时候,能观测到的一些变量直接的相关性往往是在各种复杂的因素作用下自然形成的,你强行的去改变其中一个因素,往往不见得可以一并改变跟他高度相关的其他变量。比如,最近又在微博上看到一段经典的段子:
【每天睡8小时死得更快?睡多久才最健康】这项实验长达六年时间,由加州大学圣地亚哥药学院和美国癌症学会联手进行。研究发现每天仅睡6、7个小时的人,比每天睡超过8小时,或少于4小时的人死亡率要低很多。每天睡7小时的人死亡率最低,只睡5小时的人,这个系数也低于睡够8小时的人
还有一段类似的:
华尔街统计:每天睡4小时的人,年薪基本是400万以上。多睡1小时薪水就要除以4。比如说你每天睡5小时,你就只拿400万除以4=100万年薪。睡6小时,就只能拿最多25万了。每月挣5、6千的,一般都是每天需要睡七小时的…
我承认,从心理学的角度,这个段子或许有着极强的心理暗示作用,大家要勤劳要勤劳~但是,这东西最多看着欢乐一下而已,你改变自己的睡眠时间就能改变寿命和收入?呃,目测虽不是不可能,难度还是蛮大的...
第二个问题:哪些实验可以理想地捕捉到(统计上的)因果关系?
其实在这前面,还有一个问题需要大家的思考:为什么我们需要实验?实验经济学的方法这两年扩张的非常厉害,微观计量若是没有一个随机实验(或者准实验)为基础,那么几乎要被大家argue死掉了。业界也是,搞什么新的市场营销方法若没有个随机实验来证明一下,那么结果也基本没什么太高的可信度(业界俗称单因素实验为A/B Test,如果发现某人的LinkedIn 简历上有这个关键词,不要怀疑,她很有可能是做Marketing Analytics)。只能说,太多的时候各种经济因素的联系错综复杂,谁也没办法很好的disentangle 这些因素之间的脉络关系,所以有时候不得不借助对照实验的方法来“野蛮”且“轻巧”的回答一些因果关系(只要比一下就好嘛,多简单~)。从这个角度来看,实验不是万能的,也不是唯一的灵药,但却是Simple and Elegant的。
好吧,认可了做实验这种思路,你还要考虑是不是充裕的budget去做(实验肯定是有成本的哇,而且往往成本不低的),然后有没有“道德委员会”来判决你是不是人道呢?是的,有些实验肯定是不人道的,但是我会提前告诉你么?比如莫非你不知道,当别人拿到了100元的促销红包的时候你却连个邮件毛都没看到,只是因为你在营销人员的global control list里面,压根什么邮件都不会收到么?你问我凭什么?什么都不凭,要怪只能怪randomlization。或者一个更著名的例子:米尔格拉姆实验(Milgram experiment)
实验小组告诉参与者,他被随机挑选为担任“老师”,并拿到了一张“答案卷”。实验小组并向他说明隔壁被挑选为“学生”的参与者也拿到了一张“题目 卷”。但事实上两张纸都是“答案卷”,而所有真正的参与者都是担任“老师”。“老师”和“学生”分处不同房间,他们不能看到对方,但能隔着墙壁以声音互相 沟通。有一位参与者甚至被事先告知隔壁参与者患有心脏疾病。
“老师”被给予一具据称从45伏特起跳的电击控 制器,控制器连结至一具发电机,并被告知这具控制器能使隔壁的“学生”受到电击。“老师”所取得的答案卷上列出了一些搭配好的单字,而“老师”的任务便是 教导隔壁的“学生”。老师会逐一朗读这些单字配对给学生听,朗读完毕后老师会开始考试,每个单字配对会念出四个单字选项让学生作答,学生会按下按钮以指出 正确答案。如果学生答对了,老师会继续测验其他单字。如果学生答错了,老师会对学生施以电击,每逢作答错误,电击的伏特数也会随之提升。
参与者将相信,学生每次作答错误会真的遭到电击,但事实上并没有真的进行电击。在隔壁房间里,由实验人员所假冒的学生打开录音机,录音机会搭配着发 电机的动作而播放预先录制的尖叫声,随着电击伏特数提升也会有更为惊人的尖叫声。当伏特数提升到一定程度后,假冒的学生会开始敲打墙壁,而在敲打墙壁数次 后则会开始抱怨他患有心脏疾病。接下来当伏特数继续提升一定程度后,学生将会突然保持沉默,停止作答、并停止尖叫和其他反应。
-
| 电压 |
“学生”的反应 |
| 75 V |
嘟囔 |
| 120 V |
痛叫 |
| 150 V |
说,他想退出试验 |
| 200 V |
大叫:“血管里的血都冻住了。” |
| 300 V |
拒绝回答问题 |
| 超过 330 V |
静默 |
到这时许多参与者都表现出希望暂停实验以检查学生的状况。许多参与者在到达135伏特时暂停,并质疑这次实验的目的。一些人在获得了他们无须承担任何责任的保证后继续测验。一些人则在听到学生尖叫声时有点紧张地笑了出来。
若是参与者表示想要停止实验时,实验人员会依以下顺序这样子回复他:
- 请继续。
- 这个实验需要你继续进行,请继续。
- 你继续进行是必要的。
- 你没有选择,你必须继续。
如果经过四次回复的怂恿后,参与者仍然希望停止,那实验便会停止。否则,实验将继续进行,直到参与者施加的惩罚电流提升至最大的450伏特并持续三次后,实验才会停止。
你对实验结果怎么预测?(当然现在这个实验太知名了,你可能已经知道答案了)。一般说来,大家都不会觉得人们会这么残忍对吧?其实在进行实验之前,米尔格拉姆曾对他的心理学家同事们做了预测实验结果的测验,他们全都认为只有少数几个人—10分之1甚至是只有1%,会狠下心来继续惩罚直到最大伏特数。可是结果让很多人大跌眼镜:
在米尔格拉姆的第一次实验中,百分之65(40人中超过27人)的参与者都达到了最大的450伏特惩罚—尽管他们都表现出不太舒服;每个人都在伏特数到达某种程度时暂停并质疑这项实验,一些人甚至说他们想退回实验的报酬。没有参与者在到达300伏特之前坚持停止。后来米尔格拉姆自己以及许多全世界的心理学家也做了类似或有所差异的实验,但都得到了类似的结果。为了证实这项实验,也有许多更改了架构的实验产生。
马里兰大学巴尔的摩州立分校(University of Maryland Baltimore County)的Thomas Blass博士(也是米尔格拉姆的传记—《电醒全世界的人》的作者)在重复进行了多次实验后得出了整合分析(Meta-analysis)的结果,他发现无论实验的时间和地点,每次实验都有一定比率的参与者愿意施加致命的伏特数,约在61%至66%之间。
好吧我有点跑题了,只是想说其实在实验勾画的阶段,很多东西是可以展开丰富的想象的——你先假设所有问题都不是障碍,然后去想“怎么设计一个理想的实验呢?”,然后再去依据现实的障碍做一些调整(或者可行性评估)。
有句话叫做,“被广泛应用的一定都是有原因的”,所以业界最广泛应用的A/B test肯定也是最被认可(和易于实施)的。这一类实验很简单,只要随机的一分为二,一组什么都不做(或者采用传统做法),另一组采用新的做法,然后对比结果就可以了。可是,等等,有没有觉得,很多的时候我们并不能够这么简单的实现“新做法”?是啊,我可以一分为二的发邮件,但是如果我要研究的是类似于“不同殖民统治制度对于国家解放后发展的影响?”这种话题,难道我可以让时间倒回一二百年,重新命令所有的殖民者去随机划分殖民地,然后观察后续的国家发展?嗯,就算我可以穿越时间,那些殖民者也不会听我的随机划分地盘啊——凭什么随机啊,这些本来就都是老子抢来的,老子爱怎么折腾怎么折腾。我能苦口婆心的告诉他们,“这都是为了验证殖民统治对于经济发展的结果”么?他们会在意几百年后是不是有一篇惊世骇俗的经济学研究论文发表了么?来个眼中体(点击查看大图)
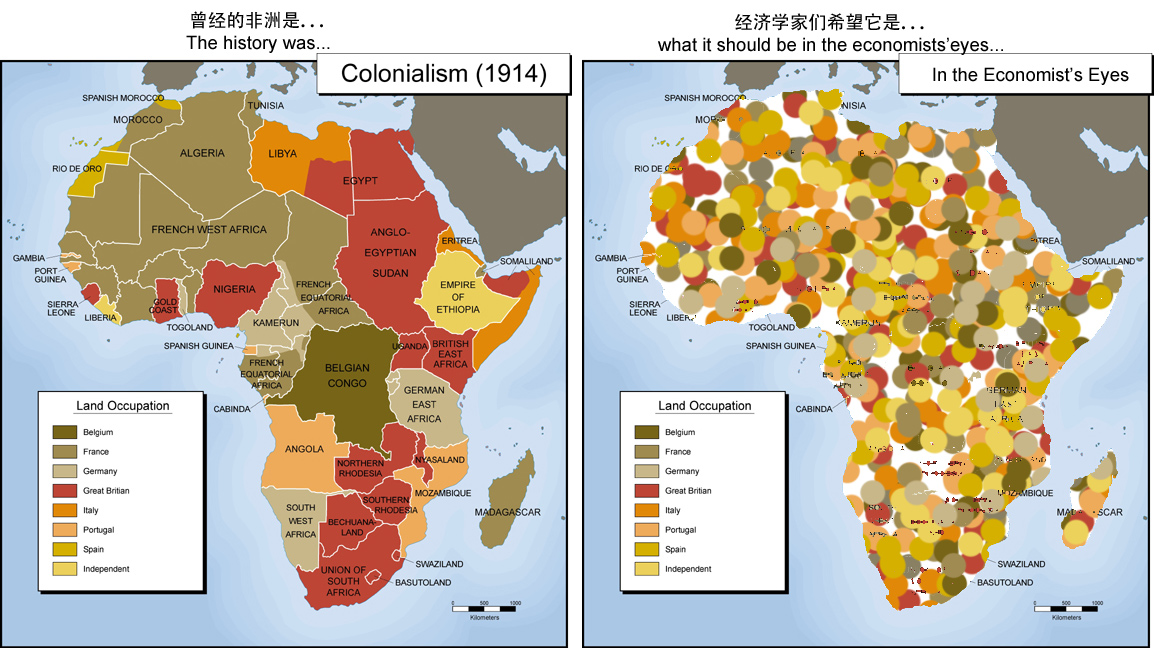
好了,恶搞够了...其实说到底,很多问题实验也是没法回答的(或者根本没法设计),这类问题我们称之为FUQ(fundamentally unidentified question, 基本上无法识别的问题)。比如,我们无法改变的还有人的性别、肤色等等(基因不是你想改,想改就能改~),不过聪明的办法是我们去改变“别人认为你是什么性别的”,比如虚构建立神马的。一个著名的例子是,2004年Bertrand and Mullainathan的paper就是虚构了简历中的肤色——改变应聘者的姓氏,然后其他工作经历等等基本一样,然后看招聘企业电面反应如何。这样的聪明的实验设计不禁让人拍手叫绝——真正起作用的到底是奥巴马黑黑的皮肤呢,还是他黑黑皮肤下面那颗白白的心呢?所谓黑白两道通吃,不外乎如此。
呃,还是认真一点,说一个本质上无法识别的问题(FUQ)吧。
比如,是不是让孩子晚上小学一点比较好?然后自然而然的,我们会想,这还不简单么?我随机找两群小孩,一群6岁,一群7岁,然后同一年入学。之后,比较他们的成绩就好了嘛。等等,你有没有觉得有什么不对的地方,这两群人本身就不一样哇。一般说来,7岁总比6岁的要更容易学习一点吧,这个搞不好是年龄因素,与入学时间其实并无关系呢。七岁的孩子无论是学一年级还是二年级的课程,应该都比六岁的孩子学得好。然后有人说了,那么就我们去看6岁上学的孩子二年级的成绩,然后比较7岁上学一年级的成绩不就好了,这样大家都是7岁呢。这不是更无语么,上了两年学的孩子肯定要多少优于只上了一年学的啊。总而言之,在这里我们没有办法区分开两种因素对于孩子的影响——是孩子年龄增长了了所以学习好呢,还是在学校的时间长所以学习好呢?如果我们真的要研究这个问题,那么显然考核的指标不应该是他们一年级的成绩,而是长大了之后比如说工作的薪酬等等。
所以说,我们一方面要让实验本身设计的精巧,另一方面也要避免去涉及FUQ类型的问题,要不就是真的自己跟自己过不去了。p.s. 另外请确保你没有漏掉什么实验过程中需要记录的变量值,要不就很痛苦了...
第三个问题:拿到实验数据以后,你的回归方程右边的X是哪些?
先统一一下名词:计量经济学里面我们更常用identification strategy来称呼用于衡量因果关系的模型。换一句通俗而不怎么严格的话,这个identification strategy就是你怎么消灭回归方程右边的内生变量(endogenous variable)的。内生变量又是怎么定义的呢?简单而不严格的来说,我们一般希望了解的是X对于Y的因果效应,即X的变化导致了Y的变化,而不是Y导致了X,所以这里需要X是不受Y反过来影响的(即X的取值的决定与Y无关——比如一个学生分在测试组还是对照组是随机的,而不是根据他的身高或年龄)。如果X,Y本身就是相互影响的,那么我们的回归系数估计值反映的只是两者的相关性(correlation),而不是X对于Y的因果效应(casual effect)。有鉴于此,我们称合格的X为外生变量(在计量经济学的定义下)。
显然,如果是随机分组实验,且X的值代表是测试组还是对照组,那么这个X肯定是外生(给定);如果我们无法证实X是严格外生的,那么就需要利用工具变量等办法来寻找和X相关但是和Y不相关的其他外生变量来完成因果效用估计,这就是计量经济学里面常说的“工具变量法”(Instrument Variable Model)。
一般说来,我们有如下几种情形:
- 随机分组实验:那么可以直接把分组变量作为X,估计出来的即为因果效应。这也就是最常见的A/B test或者multivariate test,只要保证分组是随机的。
- 自然实验:有的时候我们没法人为设计并实践实验,那么就可以借助自然界的一些外部冲击。比如,在一篇著名的论文里面,他们利用相邻的两个州之间的最低工资政策变化,研究了快餐行业就业率的影响。其实idea满简单的,就是两个州本来就业率什么的差不多,然后一个州突然提升了最低工资(类似于一个自然实验),所以去看快餐业的服务员就业情况变化就可以了(有点difference in difference的味道)。还有利用地震、原子弹什么的研究经济发展的...参见:
Card, David, and Alan B. Krueger. Minimum wages and employment: A case study of the fast food industry in New Jersey and Pennsylvania. No. w4509. National Bureau of Economic Research, 1993.和
Card, David, and Alan B. Krueger. "Minimum wages and employment: a case study of the fast-food industry in New Jersey and Pennsylvania: reply." The American Economic Review 90, no. 5 (2000): 1397-1420.不过很多时候,自然实验还是需要借助工具变量的,如果我们想测量的X始终还是有些内生性考量的。这个后面详述。
- 有条件的分组实验:这个就不是完全的随机分组实验了,有的时候我们会设一些条件,比如人均收入多少才可以申请xx补助,这样的话人均收入就成为了能不能享受政策的条件。对于这种分组实验,因为离条件很近的那些人其实也没差多少,我们假设一下连续性什么的,就可以对比他们的反应来做一些因果推断了。到时候采用的策略就是 regression discontinuity design, 即我们常说的RDD。
最后一个问题:你的统计推断模型是什么样子的?
这个问题更多的是具体问题具体分析与上述策略的结合:你需要研究的是哪些总体,什么样的样本,有什么样的一些假设?然后就是更多统计模型的问题了,比如,你是要用一般的OLS呢,还是需要robust regression(比如clustered stand errors),还是logit regression之类的。有句蛮好玩的话抄一下:
T-stat looks too good
Try clustered standard errors --
Significance gone
也好残忍是不是?至于什么时候需要用clustered standard error,后面会详细的解释。总而言之呢,随机分组实验是我们的一个benchmark,如果做不到就需要各种各样的修正方法,所以也还是蛮有挑战性的事情呢。不过我还真没在业界看到过robust regression呢...
--------------第一篇引论结束----------
另注:本连载系列可能会不定期更新,因为确实有些地方会稍稍深一些,我也得回头复习一下那些论文...只能说,这个和以往的所有偏technical的笔记都不一样,没有速成之道,只有一个个案例仔仔细细的研究下去,才可以得到一个比较全面的对于统计因果推断策略的概念。我会努力的认真的写,争取尽量少的犯学术错误...
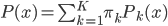 ,其中
,其中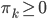 ,
,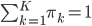 ,构成一个离散分布。同时有
,构成一个离散分布。同时有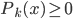 ,且
,且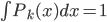 ,
,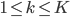 。
。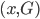 ,同时依据条件概率分布,有
,同时依据条件概率分布,有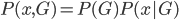 。记
。记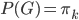 ,则
,则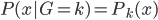 ,其中
,其中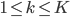 。
。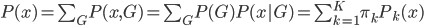 为x的边际分布。
为x的边际分布。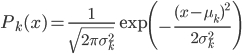 ,
,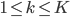 ,我们有
,我们有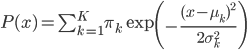 ,且
,且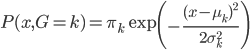 ,
,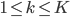 。
。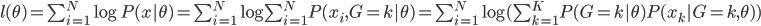 。则我们要求的就是
。则我们要求的就是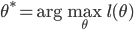 ,其中
,其中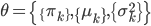 。
。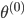 ,迭代出
,迭代出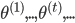 。那么问题就是,如何在已知
。那么问题就是,如何在已知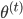 的情况下,求
的情况下,求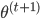 ?
?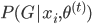 。函数形式已知,故可以求各种条件概率什么的。所以有:
。函数形式已知,故可以求各种条件概率什么的。所以有: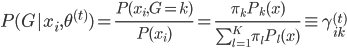 。
。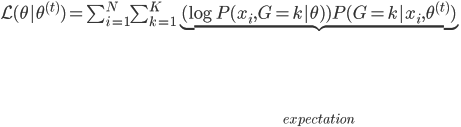 ,由于函数形式已知,我们可以计算并将
,由于函数形式已知,我们可以计算并将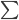 移出来,所以换成线性形式。
移出来,所以换成线性形式。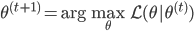 ,这样就完成了迭代。需要证明的性质是:随着迭代,
,这样就完成了迭代。需要证明的性质是:随着迭代,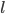 越来越大,且收敛。
越来越大,且收敛。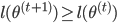 。
。
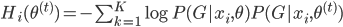 ,且
,且 ,定义为两分布的KL距离。
,定义为两分布的KL距离。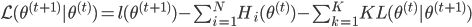 ,且
,且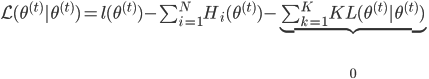 。而由M步,
。而由M步,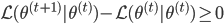 ,故有
,故有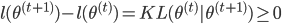 。
。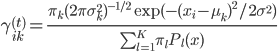 ,可以直接计算。
,可以直接计算。 。
。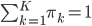 ,所以使用拉格朗日乘子法:
,所以使用拉格朗日乘子法: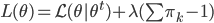 ,故有一阶条件:
,故有一阶条件: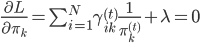 。从而
。从而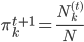 ,其中
,其中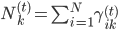 。
。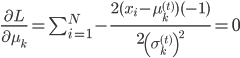 ,得到
,得到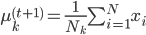 。
。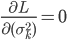 ,有
,有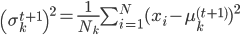 。
。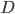 ,函数族
,函数族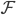 和损失函数
和损失函数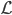 ,这样得到最优的
,这样得到最优的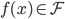 ,然后求得
,然后求得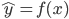
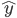 的精度如何(使用测试集)?模型的选择就是
的精度如何(使用测试集)?模型的选择就是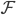 的选择,使得测试误差比较小。
的选择,使得测试误差比较小。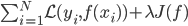 中,加入J函数来考虑函数族的复杂度,以避免过拟合。而validation就是来调正和选择这里的
中,加入J函数来考虑函数族的复杂度,以避免过拟合。而validation就是来调正和选择这里的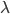 ,再用train和validation重新训练模型。
,再用train和validation重新训练模型。