Category: 读书有感

说来也有趣，这本书陪着我居然漂洋过海了好几番。我虽然对宏观属于一知半解的状态，但是对于凯恩斯这么一个传奇人物还是始终保有着足够的好奇心的。

顺手翻了一下落园以前的日志。好怀念那种读遍各种书籍的日子。那时一点点不成体系的思维，还有那种对哲学朦朦胧胧的感慨，现在都更顺利的串联起来了呢。

已经记不清六七年前第一次读这本书是具体怎样的体会和感悟了，现在重新翻开却也颇为有趣。想看凯恩斯的同性到异性恋的转变，想看凯恩斯从对于哲学和概率的着迷到参与政治事务投身宏观政策，想看凯恩斯和熊彼特的“既生瑜、何生亮”。

那就先从哲学和概率论看起吧。

这一段还是蛮好玩的。说的是老生常谈的相关性和因果关系。当年还是一个有点“群魔乱舞”的年代，大家对于统计的概念还有些模糊。从哲学的角度，对于演绎法和归纳法的适用范围和可信度还有一些争论不休。凯恩斯这里说到了计量经济学最重要的一个观点——ceteris paribus（其他条件不变），而他自己也说起来“部分均衡在实际上很难成立”，也就是就算我们的模型甚好、发现的是局部的因果关系，这样的因果关系有多少可推广性（external validity）还是需要打个问号。而有趣的是，在这个时代概率和统计还没有分的很开，大家还在从哲学的层面讨论概率存在的根基。

然后又看到一段他和拉姆齐的八卦。拉姆齐是个英年早逝的天才，想想他二十出头刚入剑桥就赶上和凯恩斯的《论概率》争论，主观概率和客观概率的争论，归纳法和演绎法的争论。

从拉姆齐的角度，归纳法是一种“思想习惯”，评价思想习惯的唯一方法就是看这种习惯是否“行得通”...不管归纳法在认识论中的地位如何， 它是一种有用的思想习惯。

这里倒是蛮契合我对于各种定量模型的评判标准...有用。很多为了追求计量上的那一点点依概率收敛、而不管估计量本身的效率如何，在我看来有点舍本逐末。今天边看边在一旁记笔记感慨，有的时候我们为了检测那么一点点弱弱的信号，投入这么大的样本量，测出来的东西不知道到底有多准。这就好像用一个超长焦的天文望远镜，追踪一颗银河系的小行星，稍不留意这行星的轨迹就没了...若不借助赤道仪等等辅助设备，真的是各种手抖。

凯恩斯和莉迪亚的八卦就不说了，对于凯恩斯来说，莉迪亚就是一枚坠入凡间的精灵吧。

前几天第一次完成了在美国的报税。因为是跟着公司搬过来的，所以有四大会计师事务所的人帮我来报税。其中需要我自己做的事情其实不怎么多。只是收到四大发过来的厚厚的72页的报税表格之后，我还是饶有兴致的学习了一番这个税是怎么算的（其实主要是因为要补税，所以在心疼我的钱...）。

以前说过，美国的个人所得税和中国最大的不同就是征缴的方式。中国的个税是在发工资的时候就按照累进税率由公司代扣了，以单人单月单笔工资收入为基数计算；而美国的税则是以家庭为单位，代扣数额需要填一张生活负担表（w-4），然后按照预期的年度收入税总额平摊到每张工资支票。这个税虽然也是由公司代扣，但是每年会有一个多退少补的环节——这也是为什么今年我会欠税...此外，在不同的就是美国的州税和联邦税是分开计算的，每个州的州税不尽相同；再者，美国有很多项目时可以抵税的，比如贷款利息、财产税、已经交过的州税等等。

我今年报税最主要的麻烦就是去年的身份有变化——从跟美国没有半毛钱关系、变成了美国的税务居民（主要的条件就是在美国呆超过183天）。在身份有变化的时候，就不能采用电子报税的方式了，而是需要把一沓报税的纸质表格寄给税务局。这种情况下，倒也不用花钱去买什么报税软件了。

结婚的话可以以家庭为单位联合报税，然而这一条跟我并没有什么关系....然后就是从银行拿到的各种利息和开户奖励什么的会收到一张1099-int表格，计入当年应纳税收入。

今年跟我没关系、但是还蛮有意思的是还有一个叫做amt的东西，我研究了半天也没搞懂我什么时候会hit amt....好像算起来还是有点复杂的。等有空的时候再仔细算一下。

 

今天扫paper扫到一篇关于美国婚姻法变化的。全文可以在作者网站上找到。

Bankruptcy and Investment: Evidence from Changes in Marital Property Laws in the U.S. South, 1840-1850

Peter Koudijs, Laura Salisbury

We study the impact of the introduction of a form of bankruptcy protection on household investment in the U.S. South in the 1840s, which predated modern bankruptcy laws. During this period, certain southern states passed laws that protected married women's property from seizure in the case of insolvency, amending the common law default which vested a wife's property in her husband and thus allowed it to be seized for the repayment of his debts. Importantly, these laws only applied to newlyweds. We compare couples married after the passage of a law with couples from the same state who married before the passage of a law. Since states passed laws at different points in time, we can exploit variation in protection conditional on state and year of marriage. We find that the effect on household investment was heterogeneous: if most household wealth came from the husband (wife), the law led to an increase (decrease) in investment. This is consistent with a simple model where downside protection leads to both an increase in the demand for credit and a reduction in supply. Demand effects will only dominate if a modest fraction of total wealth is protected.

说起来也有意思。在上海的时候，大概是正处于周围朋友纷纷结婚的年纪，加之新婚姻法的出台，耳濡目染的听到了许多跟结婚有关的话题。那个时候打开电视看上海本地的频道，到处都是结婚离婚财产房子问题的。然后才意识到，原来婚姻法竟是这么深刻的影响着婚姻的经济基础。

这篇文章有些年代了， 回溯的是19世纪四五十年代的美国南部一些州队对于婚姻法的改变。时代背景则是1841年的经济萧条、所以政府出台了破产法允许个人破产。当时的情况是，一对夫妇会作为共同的家庭财产所有者来承担对外债务，比如丈夫有外债的话那么妻子的婚前和婚后财产都会被用来偿还债务。那时很多人觉得这样是不公平的，所以南方的部分州在1846年出台新的法律条款，妻子通过财产所得的收入被认为是她自由财产。那时黑奴制度还依旧存在着，所以黑奴也是除了土地之外嫁妆的重要的一部分。有意思的是，新婚姻法适用于否是取决于夫妻结婚的时间的——如果是在新婚姻法出台之后结婚，那么夫妻就受到新的婚姻法保护和约束。

背景故事大概就是这样，然后两位作者开始用数据来实证检验当时法律变化对于家庭投资行为的影响。因为不同州通过这个新法律的时间所有区别、且这个婚姻法的只适用于新的夫妻，所以作者们可以通过对比前后的家庭投资策略的变化来得出结论。他们的数据表明，如果家庭财富更多的来源于男方，那么投资的比例就会上升；如果家庭财富主要来源于女方，那么投资比例就会降低。这样的结果也应证了他们的理论模型——针对婚姻中个体财产的保护会增加对于融资的需求而减少供给；需求效应只在共同财产受保护的时候会有作用（这个我没细看他们的模型部分，没有特别理解这里面的含义）。

所以这篇paper的故事倒是蛮简单的，实证检验部分也没有什么特别花哨的。结论倒是可以拓展到现在婚姻法的各种变化对于家庭决策的影响。感觉现在的婚姻中很多家庭格外留意对于双方自有财产的保护，提醒着我们婚姻并不是两厢情愿就可以顺顺利利的白头偕老。我曾经有段时间问过很多人，如果两个人只是希望在一起生活的话，为什么还需要结婚？仪式且不论，结婚本身不就是去签一纸合同吗？如果双方足够信任彼此，这样的纸质合约又有什么特别的意义呢？应该不会用到这份合约的那一天吧。有人说是为了孩子。那么，又为什么一定要结婚才能共同抚育孩子呢？可能大家会觉得这些问题难道问的有些可笑，这难道不是天经地义的吗？或许今日看来是天经地义的，但是这些也不是一开始就存在的，也是在人类社会慢慢演化的过程中被大家发明出来的，然后一步步修改直至如今。前段时间不是还有人说，结婚不应该是一个带违约条款的无限期合同，而可以是一个有固定年限的合同、到期双方决议是不是续约，这样大家就算处的不开心，更多的做就是要不要继续结婚、而不是什么时候离婚的决定了。

我只能说，在我有限的观察范围之内，我觉得婚姻的这纸合约更多的是对于整个社会承认夫妻双方作为一个家庭单元而存在、而不是两个人独立的存在（离婚正相反，是告诉整个社会我们俩各自为政）。比如签证、比如报税（中国的个人所得税法好像也要向家庭方向改革了）、比如买房（多少人因为限购或结婚或离婚，也是有点荒唐的可笑）。所以与其说结婚是对于夫妻双方的约束，还不如说是他们两个人决定结合成利益共同体、一致承担对外的约束。所以这样理解的话，这篇paper的结论也就理所当然了——当夫妻双方可以作为独立的财产拥有人，那么他们在整个社会群体中的角色就不是单纯的一个单位，而是两个单位了。在十九世纪当年那个男主外居多的时代，男性更多的进行着有风险的投资决策（不知道当时的具体情况，我假设女方的投资策略是相对保守的），而由于妻子不承担破产责任，社会群体给予男方的信任自然更多取决于男方本身的财产和资源。

这真的不是什么可以引以为豪的事情....我一直认为我是懂动态规划的，直到这两天重新看到动态规划的代码发现自己看不懂，然后恍然间意识到上次看懂都是7年前的事情了。google了一番搜到自己的blog真的是欲哭无泪，然后痛定思痛，觉得这次把它搞懂，重新写一篇笔记，这样万一若干年之后再回头看这个，至少保证这次的笔记有更多的含金量自己可以看懂。（更惭愧的是，高级宏观的时候天天在手动解动态规划，最多的就是无穷期动态规划，现在居然不怎么记得当年是怎么解的了...）

动态规划的用处还真多。很多例子都是斐波那次数列的，但是其实我感觉这样的例子并没有很明显的感觉。倒是今天看到一个文本排列的例子觉得很有意思，原来latex计算每行放多少词是用动态规划算的。想想word打字的时候也是不时会重排一下，所以大概也是在后面不停的算动态规划的最优结果吧。

动态规划的想法其实并不麻烦，大致就是一种以空间换时间的交换。今天耐着性子把youtube上mit公开课关于动态规划的两节看完了（19节和20节），顺便拿笔在旁边记了一堆笔记。然后找了两个例子用python练习了一番，又看了一下其他人的答案，开车回家的路上顺便又想了一下，这才觉得这次好像是想明白动态规划了。所以在这里记一下。

最短路径的动态规划解法

先来个简单的例子？路径问题好了。这个好像是最经典的动态规划例子了。我这里随便画了一个图（神器在此）。

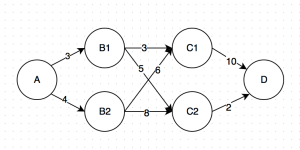
假设如同上图所示，我希望从A走到D，其中各条路径的长度已经标注在图上。那么最短的路径是哪条呢？

最笨的办法，我们可以把每条路径都列出来，一个一个走一遍呗。这里的可能性就是

• A -> B1 -> C1 -> D： 3＋3+10 ＝ 16
• A -> B1 -> C2 -> D：3+5+2 ＝ 10
• A -> B2 -> C1 -> D：4+6+10 ＝ 20
• A -> B2 -> C2 -> D：4+8+2=14

所以很显然，最短路径是第二条：A -> B1 -> C2 -> D。

那么如果问题再复杂一点呢？

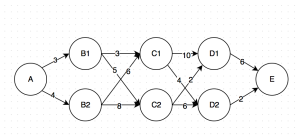这里我们还是可以继续采用笨办法，只是可能的路径多了一点：

• A -> B1 -> C1 -> D1 -> E： 3＋3+10+6 ＝ 22
• A -> B1 -> C1 -> D2 -> E： 3＋3+4+2 ＝ 12
• A -> B1 -> C2 -> D1 -> E：3+5+2+6 ＝ 16
• A -> B1 -> C2 -> D2 -> E：3+5+6+2＝ 16
• A -> B2 -> C1 -> D1 -> E：4+6+10+6 ＝ 26
• A -> B2 -> C1 -> D2 -> E：4+6+6+2 ＝ 18
• A -> B2 -> C2 -> D1 -> E：4+8+2+6 = 8
• A -> B2 -> C2 -> D2 -> E：4+8+6+2 = 20

所以很显然，第二条胜出。在这个过程中我们一共计算了8条路径、24次加法。有没有发现什么规律呢？我们其实有很多重复的计算：比如C1 -> D1 -> E我们计算了两遍。总结一下：

• 不管我们是怎么走到C1的，从C1到最后终点E的最短路径一定是C1 -> D2 -> E，距离为6。同理，不管我们怎么走到C2的，从C2到E怎么走都是8的距离。
• 这样，继续往前推，不管我们是怎么走到B1的，若是从B1到C1再到E，最短距离就是3+6＝ 9 （C1 -> D1 -> E）；若是从B1到C2再到E，最短距离就是5+8=13，所以从B1到E的最短距离就是9。同理，不管我们怎么到B2的，从B2到E的最短距离是 6+6<8+8，故为12。
• 那么回到最初的起点，A到B1再到E，最短距离就是3+9=12；A到B2再到E，最短距离就是4+12=16。

所以在这个过程中，每一步其实我们只进行局部计算就好了，不需要把各种可能性都列出来。下面是我们在每一步可以排除的路径。

 

• A -> B1 -> C1 -> D1 -> E：
• A -> B1 -> C1 -> D2 -> E： 3＋3+4+2 ＝ 12
• A -> B1 -> C2 -> D1 -> E：
• A -> B1 -> C2 -> D2 -> E：
• A -> B2 -> C1 -> D1 -> E：
• A -> B2 -> C1 -> D2 -> E：4+6+6+2 ＝ 18
• A -> B2 -> C2 -> D1 -> E：
• A -> B2 -> C2 -> D2 -> E：

这就是动态规划的力量了：在我们这个例子中，我们可以倒推出来，给定某一步的各种可能性、后面的最优走法。然后这样每次前面的只需要对比怎么走下一步、后面的最优路径就已经计算好了。

这大概是我自己对动态规划最直观的理解了：每一步都是相对独立的，所以可以先不管前面的、针对后面的进行优化、然后慢慢往前推。因为只要到了某步、后面的结果其实并不取决于是怎么到当前步的。

斐波那次数列的动态规划解法

然后看一下最著名的斐波那次数列好了，就是那个著名的数兔子数列：第一年没有兔子，第二年一只兔子，第三年1一只兔子，第四年2只兔子，第五年3只兔子，第六年5只兔子...每次都是前两年的兔子的和。

这个例子是绝佳的演示为什么动态规划体现了用空间换时间。比如我们要算第10年几只兔子，然后上面已经算好了直到第6年的兔子。我们先来看一种最笨的算法。括号里面的数字是倒推出来写的。

第十年的兔子 ＝ 第八年的兔子（5＋5+3）＋第九年的兔子（5+5+3+5+3）

第九年的兔子 ＝ 第八年的兔子 （5＋5+3）＋ 第七年的兔子（5+3）

第八年的兔子 ＝ 第六年的兔子 （5）＋ 第七年的兔子 （5+3）

 

第七年的兔子 ＝ 第六年的兔子（5） ＋ 第五年的兔子（3）

.....

一直算下去的话，为了算第10年的兔子，我们要算7次加法。这个过程中可以看出来，除了第五年和第六年的兔子是已知的之外，我们算了两遍第七年的兔子、两遍第八年的兔子、一遍第九年的兔子，然后才算出来第十年的兔子，显然是重复计算。

那动态规划这里怎么用呢？很简单啊，算过的我们就存起来，然后下一次再问到就不用算了呗；没算过的就现算呗。同样，我们已知的是｛第一年，0｝，｛第二年，1｝，｛第三年，1｝，｛第四年，2｝，｛第五年，3｝，｛第六年，5｝。

所以这个过程就是：

• 为了算第十年的，我需要知道第八年的和第九年的，然后这俩都要算。
• 为了算第九年的，我需要知道第七年的和第八年的，然后这俩都要算。
• 为了算第八年的，我需要知道第七年的和第六年的，然后第七年要算。
• 为了算第七年的，我需要知道第六年的和第五年的，这俩都知道，所以第七年是8。
• 这样，第八年的就是8+5=13。
• 这样，第九年就是8+13 ＝ 21。
• 这样，第十年就是，13+21=34。

于是，每一年我只算了一遍，算好了就存起来了，下次备用就好了。

于是有童鞋说，另外一种办法就是从头到尾算就好了嘛、一个一个往后算、到了第10年停就是了。其实这样从前往后和刚才倒推＋存储是一摸一样的计算过程、每一年只算了一遍。因为有存储的存在、动态规划会极大降低时间复杂度。不过显然最省内存的就是从头往后算了，因为我只需要记住n－1和n－2两年的兔子就可以了，不需要知道再往前的年份的。这又体现了一种相对独立的感觉：给定n－1和n－2，n跟n－3...等等就完全没关系了，想想这不就是类似时间序列中的AR(2)过程嘛！

<不过话说最高效的算法，还是通项公式吧，直接就出结果了。但那个就跟这里没关系了呢。>

强盗问题的动态规划解法

最后再来俩个比较好玩的问题吧。House Robber problem，直接复制一下别人的翻译：

你是一名专业强盗，计划沿着一条街打家劫舍。每间房屋都储存有一定数量的金钱，唯一能阻止你打劫的约束条件就是：由于房屋之间有安全系统相连，如果同一个晚上有两间相邻的房屋被闯入，它们就会自动联络警察，因此不可以打劫相邻的房屋。

给定一列非负整数，代表每间房屋的金钱数，计算出在不惊动警察的前提下一晚上最多可以打劫到的金钱数。

我们先来看一下简单的情况。

如图，这条街上一共有6栋房子，我们假设它们依次有1-6块钱。然后可行的打劫策略有：

• 打劫1
  • 打劫3
    • 打劫5：  1+3+5=9
    • 打劫6： 1+3+6 ＝10
  • 打劫4
    • 打劫6： 1+4+6=11
• 打劫2
  • 打劫4
    • 打劫6： 2+4+6 ＝ 12
  • 打劫5： 2+5 ＝ 7

所以简单计算可知，2，4，6是最佳打劫策略。在这个过程中有没有什么熟悉的感觉？比如，给定打劫4，最优的策略一定是打劫6；给定打劫3、最优的策略已经是打劫6。所以我们可以一步步倒推出来、给定某个点、往后最优策略是什么，然后往前慢慢比较前一步怎么走到这个点就可以了。其实无非就是另外一个最短（长）路径问题。

那大致思路就是：已知第i步最优策略，那么只需要比较从i-2走过来和i-3走过来哪个更优就可以了。而我们又知道，这个过程可以借助存储表来降低时间复杂度，而借助存储和从头到尾算又是等价的，所以如果采取从头到尾写的话，就是上面链接给出的代码了：

状态转移方程：

dp[i] = max(dp[i - 1], dp[i - 2] + num[i - 1])

其中，dp[i]表示打劫到第i间房屋时累计取得的金钱最大值。

时间复杂度O(n)，空间复杂度O(n)

直白的讲，就是第i步的累积最大值是比较 第i－1步的累积最大值（此时不打劫i） 和 第i-2步累积最大值＋第i步金钱（此时打劫i）。

类似的还有一个好玩的问题：

如果这些房子是相互连城圈的，就是第1间和最后一间连在一起，那么就不能同时打劫第1间和最后一间了，此时的最优策略是什么？

答案无非就是，把一个list分别去掉头保留尾、去掉尾保留头，然后分别算一遍动态规划，看看哪个是最优的就可以了。

今天就写到这里吧，希望日后回头看自己还能看得懂...