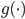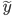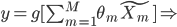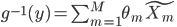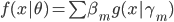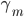此文为译文,谨此来纪念那些被R不知所云的稀奇古怪的报错折磨过的凄凉岁月...
Translating Weird R Errors
January 20, 2013
By Slawa Rokicki
原文写的很风趣,时间所限我就简单的翻译一下了。
1. 其实我只是拼错了变量名...
运行这段代码:
prob1<-as.data.frame(cbind(c(1,2,3),c(5,4,3)))
colnames(prob1)<-c("Education","Ethnicity")
table(prob1$education, prob1$Ethnicity)
然后R会报错:
all arguments must have the same length
莫名其妙有木有?其实正确的应该是:
table(prob1$Education, prob1$Ethnicity)
我只是忘了大写了...囧。
2. 我只是调用了不存在的变量....
比如我运行:
prob1$gender_recode <-as.numeric(prob1$Gender==2)
然后就会报错:
replacement has 0 rows, data has 3
但是这样就没问题:
prob1$Educ_recode<-as.numeric(prob1$Education==2)
原因只是gender这个变量不存在....你就不能直接告诉我找不到变量么?
3. 找不到变量?
我这次确保Education是有的,但是居然还是报错?
nrow(prob1[prob1$Education!=1])
报错:
undefined columns selected
而人家只是少打了一个逗号而已嘛...
nrow(prob1[prob1$Education!=1,])
哎,你就不能直接报语法错误嘛!
原文附下:
I love R. I think it's intuitive and clever and overall a great language. But I do get really annoyed sometimes at the completely ridiculous, cryptic error messages it often gives me. This post will go over some of those seemingly nonsensical errors so you don't have to go crazy trying to find the bug in your code.
1. all arguments must have the same length
To start with, I just make up some quick data:
prob1<-as.data.frame(cbind(c(1,2,3),c(5,4,3)))
colnames(prob1)<-c("Education","Ethnicity")
And now I just want to do a simple table but I get this error:
all arguments must have the same length
What the heck. I look back at my dataset and make sure that both those variables are the same length, which they do. The problem here is that I misspelled "Education". There's a missing "a" in there and instead of telling me that I referenced a variable that doesn't exist, R bizarrely tells me to check the length of my variables. Remember: Anytime you get an error, check to make sure you've spelled everything right.
If I do this, everything works out great:
table(prob1$Education, prob1$Ethnicity)
2. replacement has 0 rows, data has 3
A very similar problem, with a very different error message. Let's say I forgot what columns were in my prob1 data and I thought I had a Sex indicator in there. So I try to recode it like this:
This error message is also pretty unhelpful. The syntax is totally correct; the problem is that I just don't have a variable named Sex in my dataset. If I do this instead to recode education, a variable that exists, everything is fine:
prob1$Educ_recode<-as.numeric(prob1$Education==2)
3. undefined columns selected
Ironically, the error we so badly wanted before comes up but for a completely different reason. See if you can find the problem here. I'll take that same little dataset and I just want to know how many rows there are in which Education is not equal to 1.
So, if I want to know the number of rows of the dataframe prob1, I do:
nrow(prob1)
and if I want to know how many have a value of Education not equal to 1, I do the following (incorrectly) and get an error:
Now I check my variable name and I've definitely spelled Education right this time. The problem, actually, is not that I have referenced a column that doesn't exist but I've messed up the syntax to the nrow() function, in that I haven't defined what columns I want to subset. When I do,
prob1[prob1$Education!=1]
this doesn't make any sense, because I'm saying to subset prob1 but to do this I have to specify which rows I want and which columns I want. This just lists one condition in the brackets and it's unclear whether it's for the rows or columns. See my post on subsetting for more details on this.
If I do it the following way, all is good since I'm saying to subset prob1 with only rows with education !=1 and all columns:
nrow(prob1[prob1$Education!=1,])