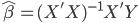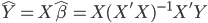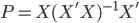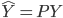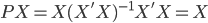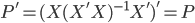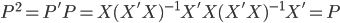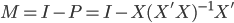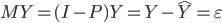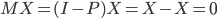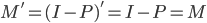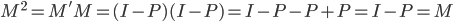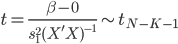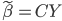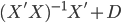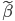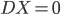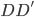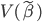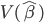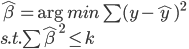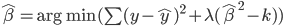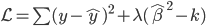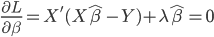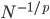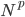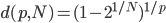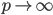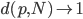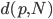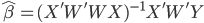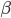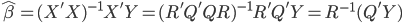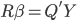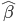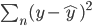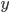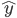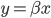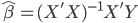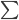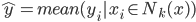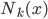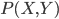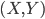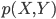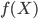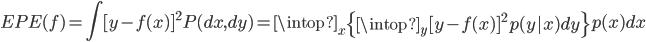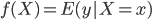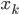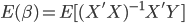众所周知的,我会经常百无聊赖的玩一些比较好玩的东西。比如画画旅行地图啦,恶搞一下COS的版猪啦,抓抓新浪围脖啦。这不R大会又要开始了么,有一点点小数据也要玩玩啦。比如,呃,君不见周六上午三场演讲都是文本挖掘的,那我不研究一下文本挖掘怎么去混演讲听啊~自己动手先。

文本挖掘自然也有有个情景嘛。这不正好会议要排日程表嘛,那得把我们16个讲座分成四个半天,每天大约4场。这个应该怎么分呢?从直觉上来说,听众肯定是希望相关的话题放在相邻的时间,这样他们就可以选择自己感兴趣的时间段去听啦,不用在那里一坐两天。同时也便于之后的集中讨论嘛。于是这个目的就是:根据演讲的题目、摘要和关键字,进行聚类。这显然是一个无监督的学习嘛,我又没有一个特定的结果变量。
那么首先,自然是要对中文文本进行分词啦。这个嘛就可以偷个懒,直接用现成的R包rmmseg4j。(中间鼓捣若干编码问题,不赘述...)
然后就是聚类。这里继续偷懒,调用现成的文本处理包tm,可以直接生成文本词对应的矩阵。比如,一个编号为1的句子是 “我 在 中国”,编号为2的句子是“我 爱 中国” 那么生成的矩阵就是:
句子 我 在 中国 爱
1 1 1 1 0
2 1 0 1 1
就是说,把每个词都作为一个变量,然后统计它在每个句子出现的次数作为变量值。这样一来,如果总共有10个句子,有不重复的100个词,那么就会给出一个10×100的矩阵了。
有了这个矩阵之后,我们就相当于知道了每个个体的观测特征,那么就可以聚类了。比较简单的,可以直接算余弦相似度(比如google识别相似新闻的做法);也可以调用kmeans聚类。这里我们的摘要直接不会有特别多的相似,所以余弦相似度的区分度可能会不好。那么就先试试kmeans吧。
到这里,代码如下:
#读数据
library(xlsx)
presentations <- read.xlsx("r-presentations.xlsx", sheetName="Sheet1") #读excel数据
summary(presentations)
presentations$Title <- as.character(presentations$Title) #转文本
Encoding(presentations$Title) <- "UTF-8" #转换编码
presentations$Title
presentations$Abstract <- as.character(presentations$Abstract)
Encoding(presentations$Abstract) <- "UTF-8"
presentations$Abstract
presentations$KeyWords <- as.character(presentations$KeyWords)
Encoding(presentations$KeyWords) <- "UTF-8"
#分词
library("rmmseg4j")
presentations$raw_word <-with(presentations,paste0(KeyWords,Abstract, sep=";")) #连接所有标题、摘要、关键字
presentations$raw_word <- with(presentations, str_replace_all(raw_word, "R","")) #去掉r
presentations$seg <- mmseg4j(presentations$raw_word) #分词
#kmeans聚类
library("tm")
presebtation_seg <- Corpus(DataframeSource(presentations[,c("Title","seg")])) #转换到tm专用格式
presebtation_term <- TermDocumentMatrix(presebtation_seg, control = list(stopwords = TRUE)) #生成词频矩阵
presebtation_term <- t(as.matrix(presebtation_term)) #转换为matrix并转置
summary(presebtation_term)
presebtation_kmeans <- kmeans(presebtation_term, 7) #kmeans聚为7类
为什么我会在kmeans里面聚成7类呢?理论上只是要聚4类嘛。可是直接聚四类的话,区分度没那么好,一半多的演讲都聚到一类去了,没法安排嘛~所以只能增加聚类的个数,看看到时候再把小类合并。
聚成7类的结果如下:
| Title |
cluster_result |
| R语言在eBay搜索引擎反馈与测试中的应用 |
1 |
| 营销分析模型及其在广告界的应用 |
2 |
| 系统生物学和转换医学中的R语言 + R in Systems Biology and Translational Medicine |
3 |
| R/Bioconductor在生物多维组学数据整合中的应用 |
3 |
|
|
| R Case Study from EBAY APD |
4 |
| 网络用户浏览路径分析 |
4 |
| 啤酒与尿布的当代版--商品分析在电子商务中的应用 |
4 |
| 基于RHadoop的关联规则挖掘 |
5 |
| 模型预测的利器——随机森林 |
5 |
|
|
| 基于R的地理信息系统 (R-based GIS) |
6 |
| R语言和其他计算机语言的混合编程 |
6 |
| ggplot和knitr包简介 |
6 |
| R与面向对象统计分析 |
6 |
| twitteR包入门和应用 |
6 |
| 短文本分类器与电商品类数据挖掘 |
7 |
| R语言环境下的文本挖掘 |
7 |
比较理想的是,聚类之后识别出来了两个文本挖掘的演讲...还有一堆R包的演讲。但是还是没法安排演讲嘛。看到这里,大家有没有发现,这样做最大的问题就是,聚类的时候把一些没有实际意义的虚词也聚类进来了,比如“的”;还有一些几乎所有演讲都会涉及的词,比如“R”和“分析”。这些词在其中是没有意义的,也会影响我们算dissimilarity的结果——这到底是按内容聚类啊,还是按作者的行文风格聚类啊?此外,虽然我们规定演讲摘要大都在100-200字,但还是有长有短,到目前我还没有对文本的出现频率用语句长度来加权...这也是不科学的嘛。那些原来在Google搜搜里面排名作弊的,不就是同样的内容复制10几次,来提高关键词出现频数(而不是频率)嘛。
为了解决这些问题,首先就是要去掉没有意义的虚词。这个不算太麻烦,把一些常用的虚词和转折词连接词之类去掉就可以了。其次,要去掉每个演讲都有的词。这里虽然可以一个个去看,不过简单一点,我们先统计一下词频嘛:
#高频词统计
presentations$seg2 <- unique((strsplit(presentations$seg,split=" "))) #断词
all_key_words <- iconv(unlist(presentations$seg2), from="UTF-8", to="GBK") #转换到GBK编码
all_key_words_fre <- as.data.frame(table(all_key_words)) #统计词频
names(all_key_words_fre)
all_key_words_fre <- arrange(all_key_words_fre,desc(Freq)) #按词频排序
all_key_words_fre[1:20,]$all_key_words #100个高频词
然后看一下TOP 20高频词:
1 的 105
2 数据 27
3 分析 24
4 和 21
5 图 18
6 在 17
7 挖掘 15
8 用户 15
9 应用 14
10 分类 13
11 了 13
12 语言 13
13 介绍 11
14 是 11
15 文本 11
16 试验 10
17 平台 9
18 ebay 9
19 案例 8
20 模型 8
所以看来,“挖掘”,“用户”,“文本”,“试验”,“平台”,“ebay”,“案例”,“模型”等等还是比较有区分度的词。按照这个思路,选择有限的几十个词重新分类,效果可能会有所改善。
此外,鉴于样本量不大(16个),所以可以人工的去看每个简介,手动标注tag作为聚类的变量。事实上,最后我还是这么做了一下,来在上述原始聚类结果上进行了一下重新的分组处理,形成了4大类。但是这个东西也不完全是可以直接用的,总要考虑时间之类的其他因素。最终的结果更多是人工思考的排序,估计李舰哥在确定顺序的时候更多的是按照经验和以往R会议的风俗。算法虽然好玩,但毕竟捕捉的还是人的思维模式,暂时没办法完美的取代吧。不过其实也差的不远呢。
最终人工结果:
冯兴东:R语言和其他计算机语言的混合编程
刘思喆:R语言环境下的文本挖掘
张翔:短文本分类器与电商品类数据挖掘
沈羽、周春英:R语言在eBay搜索引擎反馈与测试中的应用
周扬:基于R的地理信息系统
肖凯:twitteR包入门和应用
陈钢:系统生物学和转换医学中的R语言
杭兴宜:R / Bioconductor在生物多维组学数据整合中的应用
陈逸波:基于RHadoop的关联规则挖掘
李忠:R Case Study from EBAY APD
洪健飞:啤酒与尿布的当代版——商品分析在电子商务中的应用
廖明:营销分析模型及其在广告界的应用
肖嘉敏:网络用户浏览路径分析
刘成昊:模型预测的利器——随机森林
王雨晨:R与面向对象统计分析
魏太云:R基础作图与可重复研究
纯属好玩而已~不过R会议也举行了整整五届了,每次15个演讲的话也有15*9=135个演讲了。在这个样本量下,如果我们要出个论文集什么的,倒是可以直接用聚类的办法划分chapter了...嘻嘻。