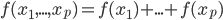继续一周一次的课堂笔记  昨天去晚了站着听讲,感觉好好啊,注意各种集中。想想整个教室里面就是我和老师是站着的,自豪感油然而生。
昨天去晚了站着听讲,感觉好好啊,注意各种集中。想想整个教室里面就是我和老师是站着的,自豪感油然而生。
第二次课讲的东西依旧比较简单,是这本书第二章的前半部分。作为一个好久之前已经预习过的孩子,我表示万分的得意(最小二乘法难道不是三四年前就学过的?话说以后我再面人的时候,就让他推导最小二乘估计量,嘻嘻...考验一下基本功)。
------------原谅我的废话,笔记开始------------
简单预测方法:最小二乘法(以下沿用计量经济学的习惯,简称OLS)
OLS实在是太普遍了,我就不赘述细节了。OLS的思想就是,基于已有的样本信息,找出一条直线,让预测值与真实值之间的残差平方和最小,即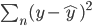 最小。其中,
最小。其中,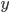 为真实的样本观测值(已有样本),而
为真实的样本观测值(已有样本),而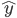 是OLS的预测值。用图来讲的话,X为一维向量的时候,就是用一条直线来最好的拟合各个样本点。
是OLS的预测值。用图来讲的话,X为一维向量的时候,就是用一条直线来最好的拟合各个样本点。
这里就很明显了,首先OLS假设是一条直线。那么就是一个参数模型,即我们需要假设一个未知的参数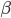 ,构成一个线性方程
,构成一个线性方程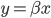 ,然后再去估计
,然后再去估计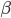 的值。然后呢,直线会有很多条,所以我们要找到一个目标——比如这里,就是最小化残差平方和RSS。换言之,我们寻找的就是最优的向量
的值。然后呢,直线会有很多条,所以我们要找到一个目标——比如这里,就是最小化残差平方和RSS。换言之,我们寻找的就是最优的向量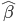 使得RSS最小。
使得RSS最小。
解这个最优化问题很简单,我就不重复了。最后解得的最优估计量为:
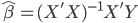
这里写成矩阵形式,比较简单。X为一维向量的时候,可以改写成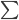 形式,我个人不大喜欢,就不展开了。
形式,我个人不大喜欢,就不展开了。
简单预测方法:K近邻(k nearest neighbor)
K近邻的思想就更简单了。不就是想预测某个点x对应的y么?那么就把它的邻居都找来,平均一下好了。不是有句话叫做什么“一个人的收入就大概是他的圈子收入的平均值么?”
所以 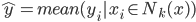 ,这里
,这里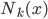 表示点x的K近邻。至于这个近邻怎么定义嘛,嘻嘻,很简单啊,欧几里德距离就可以嘛~
表示点x的K近邻。至于这个近邻怎么定义嘛,嘻嘻,很简单啊,欧几里德距离就可以嘛~
评语:吴老师对于这两个算法的直观评价是,OLS呢就是勤奋的学生,预测前先做足功课,预测的时候只要知道X,噼里啪啦一下子y就估计出来了。然而knn则是一个临时抱佛脚的学生,预测的时候开始找自己的k近邻,然后把它们平均一下就好了。哈哈,大意如此,大家可以体会一下这种精神。我个人感觉呢,OLS属于以不变应万变的,而knn则是见机行事的。
统计决策理论(Statistical Decision Theory)
说了这么多,这个模型好不好到底怎么判读呢?凡事总得有个标准呢。这一系列的标准或者说准则,就是统计决策理论了。
首先呢,大致我们需要对X,Y有个分布上的描述:用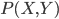 记作向量
记作向量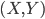 的联合分布,然后
的联合分布,然后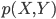 为其对应的密度函数。之后为了估计Y,我们会有很多很多模型,即各种
为其对应的密度函数。之后为了估计Y,我们会有很多很多模型,即各种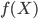 ,而这些
,而这些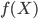 组成的函数空间记为
组成的函数空间记为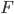 。
。
然后我们定义一个损失函数,比如在均方误差意义下,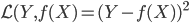 ,这样就有了一个选择的标准——使得损失函数的期望最小:
,这样就有了一个选择的标准——使得损失函数的期望最小: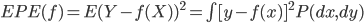 。接下来就是,到底在
。接下来就是,到底在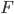 空间里面,哪一个
空间里面,哪一个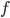 最符合这个标准呢?
最符合这个标准呢?
首先自然是把联合分布变为条件分布。这个idea显而易见——我们总是知道X的(原谅我吧,全中文确实比较难写,偶尔穿插英文一下 ^_^)。所以conditional on X,我们就有了
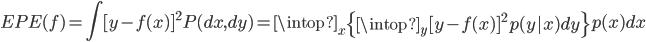
去解最小化问题,最终我们得到的就是在每个点X上, 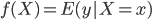 。通俗的讲就是,对于每个点预测,把和它X向量取值一样的样本点都找出来,然后取他们的平均值就可以了。很直观的不是么?这里也有点最大似然的想法呢——比如预测一个男孩的身高,最保险的就是把和它同龄的其他男孩的身高平均一下,不是么?
。通俗的讲就是,对于每个点预测,把和它X向量取值一样的样本点都找出来,然后取他们的平均值就可以了。很直观的不是么?这里也有点最大似然的想法呢——比如预测一个男孩的身高,最保险的就是把和它同龄的其他男孩的身高平均一下,不是么?
但是说来简单啊,很多时候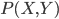 都是未知的,根本无法计算嘛。所以只能近似:
都是未知的,根本无法计算嘛。所以只能近似:
- 回忆一下knn,就是放松了两点:1)
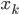 取的是x的近邻,而不一定是x; 2)用样本平均数代替了期望
取的是x的近邻,而不一定是x; 2)用样本平均数代替了期望 - 而OLS呢,也是最后在
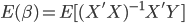 这里,用样本平均代替了期望。
这里,用样本平均代替了期望。
近似嘛,自然有好的近似和不好的近似。很显然的,当样本比较大、尤其是比较密集的时候,x的邻居应该都离x很近,所以这个误差可以减小;此外,当样本很大的时候,根据大数定律,平均数收敛于期望。所以,这两种算法应该说,都在大样本下会有更好的效果。
模型选择、训练误差与测试误差、过拟合
这里讲的比较简单。模型选择就是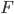 的选择,即选择哪一类函数空间
的选择,即选择哪一类函数空间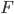 ,然后再其中找/估计最优的
,然后再其中找/估计最优的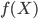 。很显然,如果只有若干个有限的样本,我们总能把各个样本用直线或者曲线依次连起来,这样的话就有无数个f可以作为此问题的解。显然这不是我们想要的——这样的称为“不设定问题”,即可能无解、可能多个解、还可能因为一点点X的变化导致整个解的解答变化。因此我们需要先设定一个解的类别。
。很显然,如果只有若干个有限的样本,我们总能把各个样本用直线或者曲线依次连起来,这样的话就有无数个f可以作为此问题的解。显然这不是我们想要的——这样的称为“不设定问题”,即可能无解、可能多个解、还可能因为一点点X的变化导致整个解的解答变化。因此我们需要先设定一个解的类别。
训练误差:预测模型估计值与训练数据集之间的误差。RSS就是一个典型的训练误差组成的残差平方和。
测试误差:用训练集以外的测试数据集带来的误差,显然我们更关心的是测试误差——训练总能训练的很好,让损失函数期望最小,然而测试集则不一定这样。一般说来,测试误差>训练误差。
过拟合:选择一个很复杂的f,使得训练误差很小,而实际的测试误差不一定小。最极端的就是刚才说的,把训练集的点一个个依次连起来...训练误差肯定是0是不是?
我们关心的自然是怎么降低测试误差。显然这东西会跟训练误差有关,但是它还跟f的复杂度有关。最最棘手的就是,f的复杂度是一个难以衡量的问题。早期的研究有用自由度来衡量这个复杂度的,但是也不是那么的靠谱...后面的有人鼓捣出来PAC(使得近似正确的概率最大——吴老师原话),还有一个VC来衡量复杂度——但几乎实践中无法计算,没几个计算出来的。嗯,水很深哇。
![]()