最近看到微博上有人提到了Bunching,因其和RDD (regression discontinuity design, 中文一般译作断点回归,也有人缩写为RD)很形似,所以好奇心起,找了相关的论文读了一下。其实很久不看方法论的东西了,满脑子想的其实都是一些实践应用的问题。Bunching却是我孤陋寡闻了,可能其主要应用的领域(公共财政)我不是特别关心吧。
计量经济学里面有很多好玩的“术”,很多都是一张图讲清楚,比如断点回归,比如synthetic control(中文有时译作合成控制法),Bunching大概也可以算作此类。昨晚通读了一下Kleven (2016)的综述,觉得还是有些有意思的地方,就和RDD一起拿出来看看吧。搜了一下,相关中文文献寥寥几篇,可能跟国内做这个方向的学者还不是特别多有关。我没有去进一步阅读中文已经翻译好的内容,可能有所重复。本篇将将作为一篇入门谈谈直觉吧。
先来一段字意和翻译的理解。Bunching这个词上来就把我打蒙了。Bunch我知道,一“束”嘛,但是在这里到底是什么集成了一束?搜了一下,中文目前翻译成聚束效应或者群聚分析法。我其实感觉这个翻译失去了英文本身的直观味道。理解了方法之后,Bunching在这里的原意更像是一个“次优陷阱”导致的集中点,即因为现实的约束,人们的选择不得不集中于一点(有点像封顶工资),从而去看密度分布的时候,形成了一个有点像离散分布的才有的mass point(在这个点对应的概率大于0)。后面会细细分解。还有两个重要的名词也在这里说说,Kink points和 Notch points。我看到这里的时候感觉我是没学过英文,完全无法代入Kink和Notch的形象化原意是什么。后面看了一下,Kink其实和数学里面的尖尖的转折点很像,比如一条直线突然折了一下,那就形成了一个突兀的Kink point,在这点肯定是连续而不可导的了。Notch则取了其缺口的意思,在这里直接断掉了,不但不可导了,直接不连续了。咦,这不就和断点回归听起来很类似吗?简单用R画两张图意思一下。后文直接用英文原词不再翻译了。
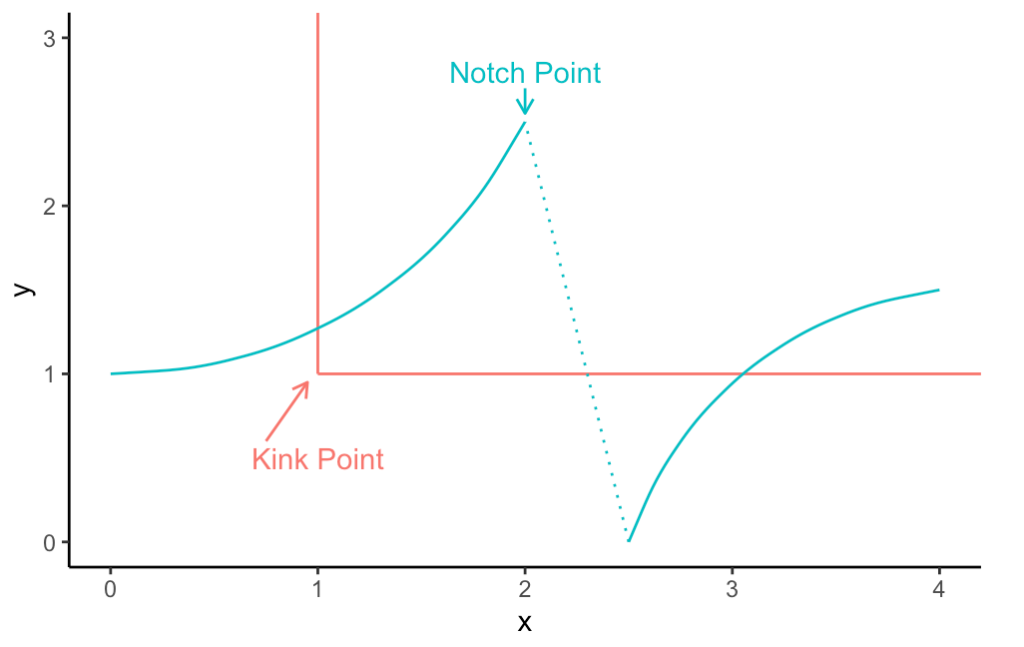 图1:Kink point v.s. Notch point示意
图1:Kink point v.s. Notch point示意在谈论方法论之前,不妨看看问题的来源。既然是经济学家搞出来的方法,那肯定是有现实问题作为背景的(上一个经济学家先于统计学家发扬光大的模型,大概要数工具变量 (Instrumental variable) 了吧?)。其实bunching这个问题来源于税收相关的研究。比如个人所得税实行的一般是梯级税率。以中国的为例,收入高出某一个阶段的部分,一般会征收更多的税率。值得注意的是,这里所说的是边际税率,而不是平均税率。超出36000但不到144000的部分征收10%的税率,但前36000只征收3%的税率,跟总收入无关。
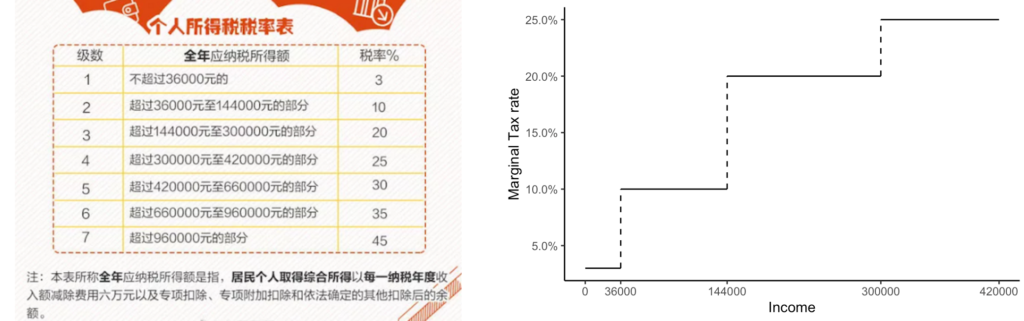 图2:个人所得税的梯级税率(左:税率表;右:边际税率示意)
图2:个人所得税的梯级税率(左:税率表;右:边际税率示意)如此的梯级税率会引起什么有趣的后果呢?最早,经济学家关心的是收入税对于劳动供给的影响。理论上,劳动者实际关心的是税后的可支配收入。如果在下一个阶梯税率过高,那么劳动者可能就会减少劳动的付出,因为边际收益(实际的税后所得)在递减,而劳动者付出劳动本身的成本可能在上升(比如加班劳动的痛苦感)。Saez(1999)年开始研究这个问题,结果这篇文章直到2010年才发表,个中故事无从探知。(题外话,Saez 2009年就拿到了“小诺贝尔奖”克拉克奖,而同一批的法国经济学家,还有去年拿到诺贝尔奖的Duflo...外加新生代的Stantcheva,法国经济学家真的是对税收研究不浅。)
Saez发现了什么有趣的现象呢?图3基本可以描述这个机制。原理大致是,对于效率更高本可以赚更多钱的劳动者来说,由于下一梯级的税率上升导致他们税后收入的减少,使得他们对于劳动投入的积极性降低。对于刚刚高于临界点的某个区间的人们来说,他们的最优选择反而是封顶在临界点(比如梯级税率改变发生在临界点1000块,那么原本可以多赚10块的人,可能就只会赚1000块而不会为了多出来的10块付出额外的努力。直觉来说,有点小富即安的意思——劳动者心想,我已经赚了1000块了,够花了,干嘛还拼死拼活多赚10块钱,大部分还要交税!)。对于那些远远高于梯级点的人,他们也会依次减少劳动产出,只获取新税率下对应的最优收入(比如上例中,原本能赚1500块的人,可能只会去赚1400块)。这样Bunching现象的产生显然是由于税率的突然变化,而劳动者等效用曲线本身却是平滑的,一小部分区间内的人便因此被挤压到一个点上故而出现Bunching了。(啰嗦一句,等效用曲线是一个经济学的概念,大致可以理解为等高线,即在这个曲线上每个点带来的效用相等,而曲线的移动代表了更高的效用水平。故而,等效用曲线和外在约束直线的切点便成为了最优选择。)
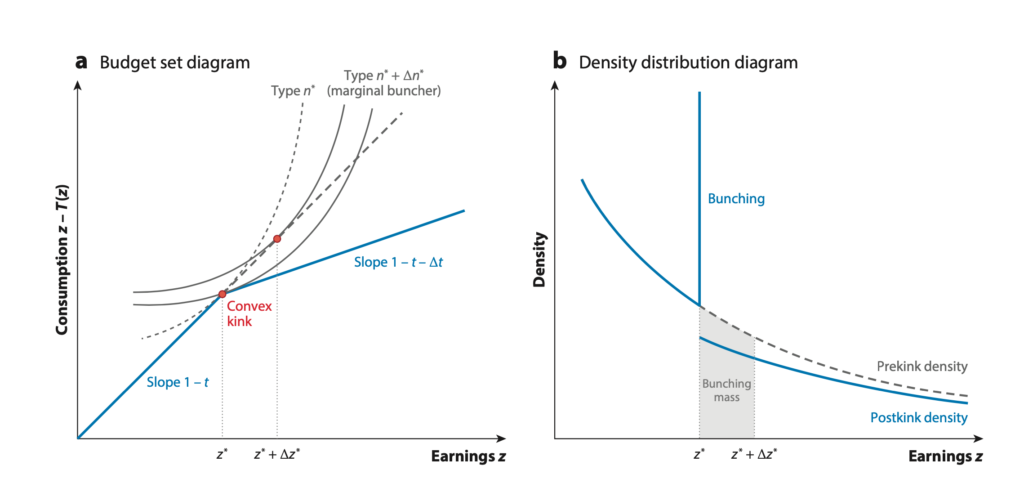 图3:一张图讲清楚 Bunching
图3:一张图讲清楚 Bunching
(左:边际税率变高使得更高效的劳动者选择减少劳动投入,封顶在kink point而不是原本最优。曲线代表等效用曲线,直线代表税收形成的预算约束;右:由于高效劳动者减少劳动投入,他们的收入在kink point聚集,直到更高效的劳动者收入下压到kink point附近,形成新的分布尾部)(图截取于 Kleven (2016),Saez (2010) 也有类似的图)图3的右图形象地描述了Bunching带来的密度函数形状的变化,也成为了学者们热衷用实证数据来量化的政策的影响。在个人所得税这个例子中,Bunching反映的是劳动者劳动积极性的降低,从而降低了全社会劳动供给量。劳动供给减少了,最终社会的生产量(比如GDP)便会降低。对于政府而言,如何设计税收梯级税率以不至于太过于伤害劳动供给,便成为了一个有实际意义的优化问题。Notch针对的问题不是边际税率会改变,而是平均税率直接改变,那么就会形成一个“洞”。在洞左边,是Bunching现象,而洞的右边,会形成一条新的曲线,所以密度函数的形状会和kink有所区别,中间会有一段“空洞”。我好奇的主要是Bunching这类方法和RDD的对比,故而在此不多赘述Notch了。
那么Bunching和RDD之间又有什么联系呢?RDD其实研究的也是政策的断点:比如去年收入低于某个临界点,才可以被选中参加某些项目。摘一张经典的Mostly Harmless Econometrics书中的配图。图4可以看出,在x=0.5这里形成了一个能否获得干预的断点:高于0.5的人获得了treatment,而低于0.5的人没有获得。在这里,我们可以认为,0.49和0.51的人原本是很像的,就是因为这个treatment的效果,才导致了他们后面结果的不同。在这个局部,我们可以将其近似于一个随机对照试验 (randomized control trial, RCT)。如果结果是跟x高度(线性)相关的(或者可以用一个函数来拟合的),那么这样的treatment effect就还可以扩展到临界点稍微远一些的地方,从而实现了一个优雅的断点回归。
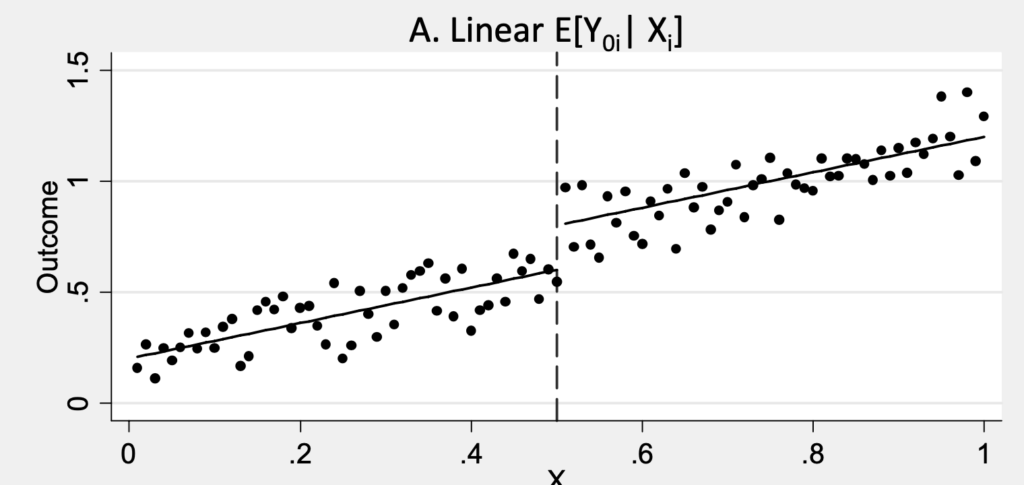 图4:断点回归设计
图4:断点回归设计
(Mostly Harmless Econometrics figure 6.1.1)值得注意的是,RDD有一个非常强的要求,就是这个用于区分的变量的本身,不能因为处理(treatment)而改变,也不能被参与的个体而选择,即外生性的要求。有了这么一个外生性的约束,我们才可以进一步做因果推断。比如身高我们一般认为是天生的,而不是后天改变,那么如果以身高作为要求来事实某些侠项目,那么就是一个外生的改变。比如最近美国因为新冠疫情而发放的经济激励补助(2019年收入在10万美金以下的可以获得一些现金),其标准是过去的收入,已经不可能因为发放激励本身而改变了,除非人们去年就能预测到今年的变化并调整收入。而Bunching恰恰相反——政策本身是事先给定的,然后观察的正是人们对这些政策反馈而表现出来的个人选择。也就是说,在Bunching这里,政策不仅不是外生的,而恰恰我们就是要观察政策作为一个内生变量对于人们选择的影响。实证层面,Bunching只是基于理论假设,直接估计密度函数本身来计算对应参数。
看到这里,对比内生性和外生约束的迥异假设,Bunching若是和RDD混淆了,那么结果可能是灾难性的。比如有些网站的会员制度是跟活跃度等相关的,高级会员会有相应特权。这时要是上RDD,那岂不是疯了?这明明是一个激励制度的设计问题啊...就是需要设计这样的制度来激励人们变得更活跃。
此外,Bunching本身在实践中也是有着很多挑战的。最重要的,Bunching现象的出现也取决于决策个体到底有多少自由来改变他们的选择。比如领工资的人相较于自由职业者,他们对于自己收入的调节能力(合理避税)就要差一些。有趣的是,类似的政策在人们更有能力控制自己选择的情况,比如股票和投资收入税方面,Bunching现象显现地便更为明显——大量的人们聚集在某几个临界点附近。
Kleven (2016) 这篇综述里面提到了其他当前应用中的局限性,比如数据本身一般是政府管理数据(例如税收),而很难用于调查数据(受限于测量误差和样本量等)。此外,理性经济人自然是另外一个因人而异的假设。第四章还提到了一些量化本身的挑战,比如kink一般比notch可能更容易肉眼看出,效果也更明显;实际数据还有一些数据本身四舍五入带来的问题。
总而言之,Bunching是一个强烈依赖于经济理论模型本身的估计方法。事先通过理论模型推导出可能导致Bunching的点,才可以进一步去量化模型中的参数。相比而言,RDD其实对于经济理论模型的要求并没有如此之高,只要外生性满足,局部的推断还是相对简单直接的。
非要一句话总结的话,不是有断点就一定可以上RDD的。如果政策或者处理有可能不是外生的,那么请一定慎用RDD。
文末附代码。