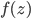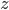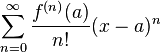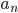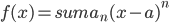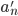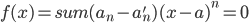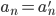有的时候会感慨,这个现实中的工作简直就是“毁人不倦”,各种工作永远是重复性无意义劳动居多,一个想法太fancy就往往不会被appreciate了。原来一个好朋友曾劝我,“今日的忍耐是为了有朝一日的 pay back”,总会有收获的时节的。但是我还是很悲哀的觉得,能不能让我不要觉得最近三年的知识积累都没有用呢?现在各种怀念写论文时候的快乐。
有个blog的好处就是可以不停的在whinning,然后若干年后可以看看自己当年到底在关注什么。刚才因为一位读者的留言翻到了两年之前学习复变函数时候写的一篇blog,看了看自己反而不记得那些是什么了。“留数”,这么一个既熟悉又陌生的概念,complex analysis算是被我遗忘的差不多了,除了“复平面”这么一个深入人心的思维框框以外。有的时候,学complex analysis, functional analysis, real analysis觉得真的是一件很快乐的事儿,不断的挑战自己的思维,但是最后,在economics里面如何漂亮的应用,我所见到的也就是那几个寥寥的著名例子。当然我承认,real analysis对于人的思维的升级和改造真的不是一个层次的,洞见力啊!
同样的,经济学里面那么多知识、模型,现在有多少又可以被我灵活的运用呢?我在不断的拷问自己。这也算是对于自己的一个考核指标吧:现在做的事情到底对未来有多大的意义。最多,也就是看看财经新闻的时候可以很不屑的对某些故意煽动情绪的分析嗤之以鼻,然后和别人纠结一下汇率、股市、房价等等其实我不怎么感冒的问题。不过,最近对我震撼最大的就是前几天去深圳玩的时候,跑到“深圳市博物馆”里面看了一下当年的深圳和改革开放前后的故事。真的,蛮有冲击力的,邓爷爷当年的洞见和魄力真的是让人钦佩万分!
这个时候才深深的意识到,上学的时候课本上一句“货币政策作用快、涉及面广”“财政政策作用慢、影响深”,即“一粗一细”之间的巨大差别。而现在,最大的争议,莫过于我国的出口退税政策吧。很简单的说,深圳的东西,出口到香港就可以享受17%的增值税返还,那么也就不足为奇为什么那么多深圳人周末去香港购物了。这么一个政策,我真的不知道它是在保护“出口加工贸易”这么一种产业模式,还是无力承受调整之后企业倒闭和失业增加的后果。可是,这个当年极大的带动了出口和就业的政策,还适应当前的国情么?我们的“内需”怎么可以承受这么一种不公平的价格杠杆呢?任何一个宏观模型,不都是以消费开始的么?没有市场价格下的消费,怎么可能有经济体的健康成长?
想到这里,觉得一个经济体的运作实在是有够复杂,一环扣一环的关系最终造就了终端产品的百花齐放。资本家会不惜一切代价的追求利益最大化,那么如果不能说服所有人、或者不存在一种可以让所有人信服的方法来维持平均分配主义,那么就应该按照市场的规则去玩这个游戏。财政政策永远是经济发展的擎肘啊。
古人云,读万卷书,行万里路。如果我应该珍惜什么,那就是在这个四处漂泊的工作中,尽可能多的体会各地的文化、经济和发展模式,然后形成自己的洞见和判断。现实总是让人意外的,以前在象牙塔确实是井底之蛙了。
最后附上几张图片:“世界之窗”里面的微缩版Park Guell和Barça的真实版 :)很有穿越感啊!
深圳版:


巴塞版: