这个是上上周上复变函数的时候和老师讨论得出的一个很简单的结论。留数是个很好玩而且很有用的东西，其中在定义了无穷远点的留数之后，有一个很好的结论：
如果函数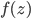 
在扩充的 
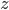平面上只有有限个孤立奇点（包括无穷远点在内），设为 
，则 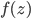在各点的留数总和为零。
这个定理在书上的证明很简单（见钟玉泉《复变函数论》第三版p232），就是做了一个以原点为中心的圆，把其他的各个点都包在了里面（如黑色圆所示，我用画图画的，效果不佳，各位凑活着看哈），只留一个无穷远点在外面，因此由沿圆周正、逆向积分之和必为0，可得结论。
当时我们就提出来，既然可以这样，那么任取一个小圆，在各个圆之中（如红色所示），那么剩下部分的积分也为零，即各个留数之和；此外也可以取一个小圆，把一个孤立极点包起来（如绿圆所示），那么也有如上的结论。
问题就在于，一定可以取到红色或绿色的小圆吗？
对于绿色的小圆，由孤立奇点的定义，必然是孤立点而不是聚点，因此必有这样的绿色小圆；那么对于红色小圆，也可以在有限个孤立奇点的情况下得证。
问题就在于，为什么这个结论依赖于有限个的约束呢？
其实由孤立奇点的定义，我们可知，不可能存在无限个孤立奇点——在把无穷远点视作一个点的时候。否则，画一个大圆，内部有无穷多个孤立奇点。而无穷点列在有限闭集内必有聚点，因此与孤立点的定义矛盾。因此，我们只能讨论有限个孤立奇点的情况。
事实上，从另一方面看，留数本身的定义就依赖孤立奇点，因此若是无限个则必有聚点的前提下，留数的定义就不存在了。因此，这个结论也就毫无意义了。