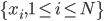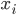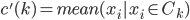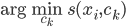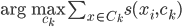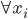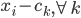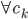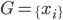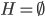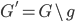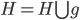最近一直在看Community Discovery这一块儿的论文,深深的感觉现在就是一个矿工,不断的想方设法挖出来更有价值的信息。而且不是一个点一个点的突破,而是需要寻找出一种脉络,串联起所有的信息来。头痛。
最近的情况是,有一个well-connected的网络,然后我想把它稀疏化、打散成一个个独立的community的感觉。这样就可以分别识别每个community的特征什么的。所以厚着脸皮找施老师讨了几篇papers。而主要的问题是,数据太大了...11M nodes, 20 M edges,还是directed weighted network...我直接放弃了把这些数据从SQL Based data source中挪出来的想法,还是先努力的减少一些edges吧。
先罗列几个相关的术语:community discovery, graph partitioning, network clustering, network sparsification, modularity。了解一个领域最好的方法大概就是去读literature review了,所以乖乖的要了一篇:
Srinivasan Parthasarathy, Yiye Ruan and Venu Satuluri. "Community Discovery in Social Networks: Applications, Methods and Emerging Trends", in Social Network Data Analytics 2011. (NS, DM)
最契合我的想法的就是cut类方法——remove some edges to disconnect the network, then (drop isolated nodes with degree = 1 (could be added back later as auxiliaries to each community)。
那么就先从这一类方法开始说。比较经典的算法呢,是希望砍掉一条边以后,community内部的凝聚力不变,外部连接变差。基本上常用的就是Ncut(normalized)和Conductance、KL object、Modularity这些指标。比如KL算法,就是从二分图开始,不断迭代的去寻找如果交换某两个点所属community就可以减少edge cut的边。可惜的是,这些最优化问题都是NP-hard....随着数据的增大算起来会异常吃力。KL算法本身迭代也是相当考验计算能力的(贪心搜寻)。
然后就是凝聚(或者切分)类算法。凝聚就是先各自为家,然后附近的相互结合在一起,直到理想数量的社群结成;切分则是先从一个整体开始,然后每一步都切成两份这样。这些都算是层次聚类,最后可以给出一个长得像二分树的系统树图。这一类算法有Girvan和Newman切分法:每一步先计算每条边的betweeness score,然后把得分最高的边砍掉,然后再重复这个步骤。嗯,问题依旧是这样的迭代很耗时间。
频谱类算法(spectral algorithms)。听这个名字一股经典风就袭面而来。基本上这类方法就是仰仗特征向量(eigenvector),比如adjacency matrix的特征向量,然后top k特征向量就定义出来一个k维的特征空间,然后就可以用传统的比如k-means这样的方法来聚类了。说白了就是降维、降维。可惜这种方法依然算起来很消耗资源,光算那个特征向量就是O(kM(m))的复杂度...基本在大矩阵下就投降了。一个概率的方法就是Graclus算法,基本的直觉就是基于加权的normal cut measures再做加权核k-means便可以给出基于特征向量聚类一样的结果,而计算消耗相对少一些。
多层次图分割(Multi-level graph partitioning)。这个就是相比而言快速有效的方法了。基本的想法就是,先压缩原始图像到一个小的图像、分割这个图,然后再映射回原来的图。毕竟小图分割起来就要快的多嘛。这类的方法除了上面说到的Graclus,还有Metis(以KL object作为measurement),以及MLR-MCL。
马尔可夫聚类(Markov Clustering,MCL)。基本的想法就是,两点之间的信息传递是随机流(stochastic flow)。MCL对随机矩阵会做两个操作,扩张(expand)和膨胀(inflate)。前者就是简单的矩阵平方,后者则是用一个膨胀参数(非线性)来撑大彼此之间的差距,最后再重新normalize。这两个步骤交替进行。这样的话,原本community中紧密相连=的两个点则会更紧密的相连,而不同cluster之间的连接则被弱化。这样最后每个community之内的点都会流向某个attractor(吸引点),从而我们可以识别各个cluster。感觉这里有点收敛到一些不动点的意思。MCL的弱点也是计算消耗。矩阵乘法在开始边的权重没有弱化的时候是非常消耗时间的,此外MCL倾向于产生不平衡的群落,尤其是可能产生一堆很小的群落或者一个很大的群落。
MCL的改良主要是在引入惩罚项(regularized MCL)和加入多层次(multi-level regularized MCL),以减少不平衡的clusters和解决MCL难以scalable的问题。后者也简称为MLR-MCL,就是刚才多层次分割里面有提到的那个。
局部聚类(local graph clustering)。局部方法基本上就是从一个给定的顶点(seed)出发,寻找符合条件的群落,而并不关心整个graph的情形(除非所有的群落需要覆盖全图)。计算上就是利用随机游走(random walk),从一个群落的内部开始,一点点的向外扩张(有没有很像page rank的感觉?)。最早的Spielman and Teng就是这样的基于顶点随机游走的算法。后面Andersen and Lang改进了这类方法,可以从一堆seed sets出发而不是单单一个顶点。此外,Andersen还试图在随机游走之上加入re-start(即个性化的pagerank)。
再需要提及的就是在动态网络(dynamic network)之上的community discovery——不同于静态网络,动态网络是本身一直在变化的,正如我们一直在用的facebook、twitter这般。还有异质网络(heterogeneous network)和有向网络(directed network)。呃,这部分我就没细看了,貌似蛮复杂的样子...就是其中有一个Community-User-Topic(CUT)model看起来蛮有意思的,准备明天去找这篇paper读一下:
D. Zhou, E. Manavoglu, J. Li, C.L. Giles, and H. Zha. Probabilistic models for discovering e-communities. In WWW ’06: Proceedings of the 15th international conference onWorldWideWeb, page 182. ACM, 2006.
嗯,到总结了~前面一直在说的就是计算、计算、计算。
- 可扩展的算法(scalable algorithms):这里主要是牵扯到分布式计算。multi-level类的算法是有分布式的潜力的,然后GPU和多核计算貌似也能对流算法(streaming algorithms)帮上忙。
- 群落和其进化的可视化:可视化主要是可以帮我们更直观的理解动态网络的变化、提供分析的直觉、以及帮助验证分析结果。
- 结合业务知识:这个也不仅仅是对这些群落识别算法啦,任何一个机器学习的算法都离不开基本的业务知识吧。
- 排序和加总:基本上还是缺乏对于得到的群落之间的排序(打分)、加总的研究。
好了,到此为止~继续看其他paper去了。