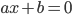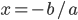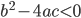从简单的统计模型,到后面的计量经济学,到机器学习,到现在的人工智能,过去的二十年是归纳法大发展的二十年。为什么只看二十年呢,因为二十年前的园主不知世事,超出认知范围之外了。
经济学在大规模应用计量经济学之前,一直是和物理学神似的,也被叫做社会科学中的物理学。而计量经济学的发展与突破也不是纯属巧合,主要是大规模经济金融数据的爆发。
早期的计量经济学,无论是宏观还是微观,其实都还是有深深的“结构化”的影子,就是需要一个结构化的模型来解释为什么会这样,有一堆变量和与之相对的系数,然后再用数据来估计系数。现在回头看,这个时期的计量经济学还是停留在一个“辅助”的阶段,数据的价值只是帮助计算系数。
然后计量经济学就向着弱结构化的方向一去不复返。可以说这是理论的发展赶不上数据的爆发,也可以说是人们渐渐失去了对结构化的理论的执念。这大概等同于量子力学之于传统物理学的革命,人们开始接受这个结构的模糊化。可就算是在这个阶段,人们的执念还是“因果关系”,直到今日计量经济学还是把因果推断作为其存在的哲学本源,试图从归纳法的角度倒推演绎法需要的因果关系。
然后随着机器学习的大爆发,人们从开始的“预测”和“因果推断”是两回事,到逐渐的审问自己,为什么对因果有这么强烈的执念?退一步说,到底什么是因果关系?这个时候才发现,因果关系其实在哲学上的定义也不是那么得清晰。园主在这里就不挖太深了,否则填因果这个坑就要填好久。
这些年,随着大语言模型的爆发,人工智能好像又解锁了一个新的阶段。虽然一边说着大语言就是一个预测方向无意的突破,另一边园主却看到人工智能落地层面对于结构化关系的依赖性慢慢减弱。以前我们的解决办法是对一个问题不断地细分梳理,然后逐个攻破。而现在大模型的冲击就是,我们真的有必要这样分解问题本身吗?如果深度学习模型本身可以就自动学出来一个等同于以前结构化的东西,就算我们没有办法把它明确的表达出来,哪又如何呢?
到这里,深度学习无疑是冲击到一个哲学层面的问题。当数据远远超过了理论的发展的时候,是不是演绎法的价值就远远不及归纳了?我们是像以前那样路径依赖,一定要对问题做一个外科手术一样精准的分解,还是可以容忍结构慢慢演变成一个黑盒子,给它无尽的自适应的能力,然后只需要关注结果就可以了?
这一波深度学习对于人工智能的冲击,我觉得体现到最后, 其实可能是一个去结构化的冲击。我们选择放弃对于结构关系的清晰表述,然后拥抱强化的预测能力对于世界的适应和改造。
人们对于深度学习和大模型的恐惧在于我们无法解释、进而无法控制。一旦我们适应和接受,下一步就是挖掘其无尽的潜力,实现下一轮生产力的爆发。
无论如何,我还是看好科技发展与世界进步的,就算过程中会有无尽的波折。