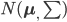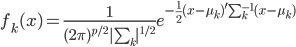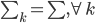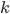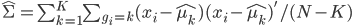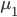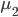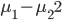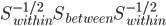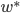Tag: 模型

Categories
读书有感

捉襟见肘补数学

前几天跟家父闲扯，说到我这辈子为数不多后悔的事情，就是本科选专业没选数学。我的性子基本上是不会多想过去已经发生的不可改变的事情的，所以人生中还真没多少后悔的事。这件事情是例外，是因为从毕业以来一直在为其还债，不得不怨念一下。当然，确实很难讲如果我当时学了数学，现在会不会过得更好。可能也不会。

假设过去未曾发生的事情没什么意义，不如讲讲为什么让我这么怨念。前几天在查一个模型，想知道一些大样本特性那边的结论，于是开始翻看相关的论文。结果论文读着读着就读不下去了，因为根本看不懂其中的引理。不仅仅是证明看不懂，而是根本不知道为什么要用到这些引理，这就很尴尬了是不？回头查了查，这些基础知识都是渐进理论那边的，属于概率论吧，确实没有学过，不知道就是不知道。

这种捉襟见肘的感觉实在是太熟悉了。去年看另外一个方向的论文，发现根本没学过concentration相关理论（这个名词不翻译了），然后现学现卖，抓紧去补那块儿的知识。然后看到Lipschitz 连续性，完全不记得实分析怎么讲的了，又得回头复习。为什么不记得呢，还是因为当年没理解，没有把数学融会贯通成自己的思维，自然考完试就忘了。不过至少因为学过，所以复习总是比重新学习容易一些，而且这次看到应用了也能加深对其本身的理解。数学虽说是个工具，但是如果不记得工具怎么来的可以怎么用，那要么就只能望洋兴叹，要么就闭着眼瞎用。鉴于后者着实不是我的风格，大部分时间我都只能止步之后扼腕叹息。

说到底，之所以数学让我这么痛苦，还是很多东西学的时候没有成体系，用到什么补什么。像微积分啊线性代数啊这种还好，宏微观计量各来一遍，到后面怎么也不会忘了。但是其他的不常用的就惨了， 只能两眼一抹黑，实在不行就死记硬背吧。我挺佩服那些随时可以从一个阶段捡起数学直接用的人，他们不需要知道下面的基础是怎么架构的，只需要往上盖就行。我受不了这样，对我来说数学一定是一以贯之的，若是我不曾理解基础那我就永远没法继续往下走。当然我可能不会一直记得每一个细节是怎么样子，但大体的脉络永远是清晰的。

可能事情并没有我想象的那么糟，我的数学知识也不是哪里都是窟窿永远填不完。但这种不知道我还有多少窟窿没填的状态，让我大部分时间都没有底气，特别惧怕又发现一个窟窿那种沮丧感。毕竟一直处于一种“追赶”的感觉会让人自信全无。若是曾经在本科阶段按部就班地训练过，或许就不会像现在这样不安了。比如看经济学我就不会不安，因为我知道自己的基础很牢，一切新生事物都是基于以往一些问题的拓展，这给了我很足的底气来辩证地学习新知识（以及看到胡说八道的理论知道他们是在胡说八道）。正是因为有这两者完全不一样的状态的对比，我才无法控制自己的怨念。

======

题外话，本科专业没选数学完全是当时的无知。按说我一个高中生无知就罢了，我得到的各种指导信息居然都是，“大学数学和高中数学不是一回事儿，高中数学再好大学数学都有可能让你失去兴趣。”之类。居然没有一个人告诉我数学本身对于其他基础科学是有多么重要。感觉数学教育出了很大问题，让前面学过数学的人并没有体会到数学的基础性和重要性，自然也就无法告知后来者。当然，从家父的角度，他觉得稳妥最重要，数学一看就是一个找不到工作的专业。我不否认，从现在来看确实很多数学专业学着学着就走进死胡同了。但更重要的是，我的性格决定我并不会安于现状，而除了数学之外，怕是少有一直能给我足够的智力挑战的东西了。那种从抽象层面理解事物的满足感，那种一脉相承融会贯通的舒畅感，至今不曾从别的事物上体验过。性格决定命运，所以虽然对于大多数人来说，本科学数学或许并不是一件好事，但对于我来说，却导致了十几年来的最大缺憾。

Categories
经济、IT观察与思考

一些观察

随便写写，随便看看。

1. 关于研究方向。

读的paper多了，发现大多数人的研究路数无非两种：

  • 一种是锚定一个问题，然后用尽各种办法来看哪种可解。换个通俗的就是，车坏了，找出一堆工具来看看怎么可以修好。
  • 另一种则是，沿袭一套方法论的路数，试图解决越来越多的问题。通俗的讲，就是木工不满足于打打家具，还要去试试电工水工装修工。

你说孰优孰劣？没有高下之分。谁也说不好一篇好的研究到底是问题导向的还是方法论导向的。不过鉴于一般来讲方法论比较容易训练出来，所以有的时候看似包装的很漂亮的paper可能正是这个方法灵了然后倒回头来包装问题本身。

本以为这个只是看paper时候的感觉。后面发现，工作其实也不外乎如此。有的人凭着一门专业技能，比如编程，就可以在不同部门之间切换来切换去，反正总有需要用到编程的地方。有的人有一些具体问题，然后就广撒网找来各种背景的人帮忙解决。前者最后进化为技术专家，后者进化为大BOSS。

2. 关于建模

说到模型，反正上来都是那句至理名言：

没有模型是正确的，只有一些是有用的。

所以一切试图证明自己是真理的模型都是无用功。如果是真理，搞成体系那就叫他理论，可以慢慢证明就叫做定理，不证自明那就叫公理好了。反正我觉得说某个模型是正确的这种言论都是挺无聊的。

基于这一条，在实际商业环境中建模，就不要一开始给自己摆太高的期望。就跟上面说的，很多时候问题都是第一类人发现的，他们只是寻求有着不同技能的第二类人帮忙看一下，实践中谁好用就用谁。所以一群第二类人内部争来争去，什么机器学习流派啊、数理统计流派啊、计量帮啊、物理统计帮啊还是算命仙人这些其实都不那么重要...比如最近世界杯大家都在预测，那么不管你是章鱼还是小丸子还是霍金，只有预测对了大家才信你。

所以在学校里被某个流派洗脑洗的深入骨髓的，可以醒醒了。不要一上来就摆出自己是真理这样的架势。每个人在象牙塔里都是这么教的。

3. 关于统计建模

如果大家笃定就要用统计的方法了，那么要解决的问题就无非是：搜集数据（变量）、选择模型、修改参数以达到最优。

具体到项目，搜集数据这个肯定是大头。每个学过统计的都被教导过“garbage in, garbage out”。只可惜大部分老师讲完这句话之后，学生并没有多少机会实际的去搜集数据，或者更直接的去想要怎么搜集数据。大部分学校里面的训练（尤以网上数据挖掘竞赛之时）都是，数据集给定，怎么找个更好的模型来预测/评估/解释。真到了项目上需要搜集数据了，大部分人的做法无非就是先找张纸把想到的变量都分门别类列出来，然后把所有可能拿到的数据都扔进去试试，从简单的线性回归或者分类器开始，到非线性的各种模型都扔进去跑一遍，反正这年头计算能力不是瓶颈，总有合适的模型自己可以去做变量选择。

听到这里，貌似也挺好啊。是啊确实没什么不好，如果大家都有充足的时间慢慢玩的话。可惜的就是这种无脑流在大多数情况下都是受制约于时间的。于是为了省时间，要么就某些麻烦的数据不搜集了，要么就某些计算复杂的模型不去跑了。差不多就好了。解决问题了么？可能也差不多解决了70%-80%。

与此同时还有一类业务流派。这类人特别像医生似的，是某个具体领域的专家，专到什么程度呢？基本上他熟悉的地儿有个风吹草动都逃不过他的眼睛。直觉很准，或者说经验实在是太丰富了。跟这个流派的人一起工作很好玩，他们想到一个问题大概的给你指一个方向，大部分情况下八九不离十，差不多就可以把问题解决了。就算事后需要稍微建建数理模型多做一些分析和验证，基本也不会太麻烦。每当此时，不禁大呼一声畅快，瞬间觉得自己以前的思路真实的麻烦爆了。嗯，爽归爽，不过这种流派需要在一个领域浸淫比较长的时间，逃出他的领域就比较难说了。

4. 关于这些碎碎念

基本上就是想说，容易训练出来的都是不重要的...那些东西都进化很快，学术界不是白白养了一群人浪费的（虽然也挺浪费的），所以长江后浪一定会把前浪拍死在沙滩上。

与此同时，业务知识也不是那么重要的。经济环境变化太快，谁也不知道明天这个世界会变成什么样子。

那既然都是以不变应万变，那还是选一条比较开心的路子。总是需要合作的，这个世界已经复杂到没有可以一个人解决的问题了。

Categories
读书有感

≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记（五）

鉴于我上周写的[笔记（四）]让很多人反映太枯燥、太无聊（全是公式...可是这就是笔记嘛，又不是写科普文），我努力让这周的笔记除了公式之外多一点直觉和应用层面的点评。

其实[笔记（一）到（二）]中说了很多回归和分类器的不同了，那么在经历了线性回归方法之后，就来说说分类器好了。我原来一直觉得回归和分类器没有什么本质不同的...主要是最常用的分类器logit和probit都是我在学计量的时候学的，那个时候老师只是简单的说，这两个和OLS都是一致的，只是我们想让预测值在0～1之内所以做一下变换。而且我们那个时候也不叫他们分类器，而是叫他们“离散被解释变量模型”。前几个月的时候，看data mining的东西，看得晕晕乎乎的，就跑去问精通此类模型的同事MJ，让他跟我科普了一下午为什么这两个模型大家更经常称之为分类器...汗颜啊，那个时候我才知道原来machine learning是先分supervised learning and unsupervised learning，然后才是 regression v.s. classification, and clustering...疏通了脉络之后，再看《The Elements of Statistical Learning》这本书，就觉得顺畅多了。以前只是零零散散的接触一个个孤立的模型，没有找出一个脉络串起来过，自然也就不知道分别适用于什么场景。

其实我挺想说的是，从econometrics到data mining，远远没有想象的那么简单。数学工具上或许很顺畅，但是思维上的转变还是需要时间和实践的。真是为难坏了我这个学经济学出身的孩子（其实话说回来，我好好的不去研究经济学，好奇什么data mining呀~只能聊以一句“殊途同归”来搪塞自己，对嘛，反正都是doctor of philosophy, 只要是科学，本质的思考方式应该是相通的）。不过搞清楚之后，还是觉得很好玩的——以前是雾里看花，觉得什么都漂亮；现在渐渐的能够分清楚这些美丽之间的差异了，也算是个小进步吧。

再有个小废话...记得上小学的时候，老师问大家“长大了想做什么呀？”，我们总是会特别有出息的回答“科学家~”。那个时候有门课叫做《自然》，老师总给我们讲各种各样的发明，让我们一度觉得这个世界上的问题都被解决完了，还当什么科学家啊。然后老师就给我们讲哥德巴赫猜想，大意是世间还有那么几个悬而未决的皇冠问题，等待大家长大了去攻克。后来，越读书越发现，有那么多问题人们是不知道答案的，只是从 ambiguity -> uncertainty -> possibility -> probability -> certainty (law)一步步的走下去。有那么多问题，其实都是悬而未决的哲学问题，等待着聪明的大脑去回答。这也是越读书越觉得兴奋的缘故吧，越来越多的时候老师会被问倒，然后说“不知道”...然后好奇心就又开始勃勃生长...然后又发现更多的很好玩但没有答案的问题...周而复始，有意思的很。

-------满足大家的八卦之心之后，笔记开始-------

线性分类器

对应原书第四章。

先是来一点直觉上的东西：分类器顾名思义，就是把一堆样本归到不同的类别中去。那么这类模型的几何直觉是什么呢？很简单，空间分割嘛。最直白的，我们有一群人，组成了一个大的群体。然后现在要把大家归为男女两类，那么空间自然就是被分割为两个子空间——男和女了。

线性分类器是什么呢？分割男和女的时候，可能分割是三个一群，五个一簇的，所以非要画分割的界限的话，八成是山路十八弯的...我们以前说过，这类的模型问题就是可能复杂度比较高（比如参数的个数较多），导致就算训练误差小，测试误差不一定小。所以呢，我们希望这个分割界限是直线的（二维平面下）、或者平面的（三维空间中），或者超平面的（高位空间中），这样就比较清晰明了的感觉了。

线性分类器：logit模型（或称logistic regression）

这里也不完全是按照吴老师上课讲的东西了，因为回头再看这本书会发现书中还有一些很好玩的直觉很强的东西。错过不免可惜，一并收纳。

首先换一下记号～我们在前面都用代表被解释变量，从现在开始对于分类问题，我们改用。

logit模型下，考虑最简单的分为两类，我们有

所以有

这样，分别属于这两组之间的比例就可以找到一个线性的边界了（注：log为单调变换~不影响结果）。这样变换的目的其实无非是，保证，而且两个比例之间存在着一种线性的、或者可以通过单调变换成为线性的关系。类似的当然是大名鼎鼎的probit模型，思路是类似的。

损失函数

显然线性分类器下，在有很多类的情况中，损失函数定义为OLS的残差平方和是没有多大意义的——分类取值只是一个名义量。所以，这里用0-1损失函数：如果，那么损失函数=0；否则，就是没预测准，损失函数=1。写为数学形式，就是损失函数定义为：

所以我们的目标就是，最小化损失函数的期望：

(条件期望迭代)。

LDA：linear discriminant analysis(贝叶斯意义下)

从贝叶斯的角度，我们有，

为k出现的概率。

假设X服从联合正态分布，那么我们有。

再假设协方差矩阵，所以我们比较两类和的时候有：

这样就形成了一个x的线性方程，所以我们找到了一个超平面，实现了LDA。

实践中我们需要估计联合正态分布的参数，一般有，其中为分类k出现的样本数；，即这个样本中，x观测值的平均数；。

Fisher视角下的分类器

Fisher提出的观点为，分类器应该尽量使不同类别之间距离较远，而相同类别距其中心较近。比如我们有两群，中心分别为

和，那么我们希望尽量大，同时群内方差

尽量小。通过对x进行投影到，我们可以化简的得到

且。这样一来，我们的准则就是：

由于是正定阵，所以我们可以进一步写为

其中是的特征向量。最终可以求的，最优的正是的最大特征向量。

说实话，我对LDA（或者QDA）的理解都非常有限...这本书里面还有一节说到LDA和logit怎么选，我也是大概看了一下没有特别的看明白...笔记只是如实记录，海涵。暂时还不知道讲到Fisher到底是想讲什么...理解力好有限，唉。

------最后的碎碎念------

除了统计学习精要，Coursera的Model Thinking也终于结课了，做完了期末考试卷，感觉心里空空的。这门课真的是开的非常深入浅出，覆盖了这么多学科、问题的各种模型，非常有助于逻辑思考和抽象。只是多少有些遗憾的，很多东西来不及细细回味，听过了视频就忘了，没有努力的去理解那些模型背后的逻辑。这也是导致最终的期末考试做的不怎么好的缘故——我不想去翻课堂视频或者笔记，只是想考验一下自己对于这些模型的理解和记忆能力。事实证明，除了那些跟经济学或者数学紧密相关的模型，其他的都多多少少记得不是那么清晰了。过阵子应该好好整理一下这门课的笔记，算作是一个良好的回顾吧。

不知道为什么，工作之后再去学这些东西，真的感觉力不从心的时刻多了很多。这半年只有这么区区两门课，就让我觉得有时候不得不强迫自己一下赶上进度，强迫的手段之一就是在落园开始写连载（大家容忍，谢谢~）。不过为了保持一个基本的生活质量，还是应该不时看看这些新东西的，要不生活都腐朽了。

Categories
游来游去

沿着数学的思维

有的时候会感慨，这个现实中的工作简直就是“毁人不倦”，各种工作永远是重复性无意义劳动居多，一个想法太fancy就往往不会被appreciate了。原来一个好朋友曾劝我，“今日的忍耐是为了有朝一日的 pay back”，总会有收获的时节的。但是我还是很悲哀的觉得，能不能让我不要觉得最近三年的知识积累都没有用呢？现在各种怀念写论文时候的快乐。

有个blog的好处就是可以不停的在whinning，然后若干年后可以看看自己当年到底在关注什么。刚才因为一位读者的留言翻到了两年之前学习复变函数时候写的一篇blog，看了看自己反而不记得那些是什么了。“留数”，这么一个既熟悉又陌生的概念，complex analysis算是被我遗忘的差不多了，除了“复平面”这么一个深入人心的思维框框以外。有的时候，学complex analysis, functional analysis, real analysis觉得真的是一件很快乐的事儿，不断的挑战自己的思维，但是最后，在economics里面如何漂亮的应用，我所见到的也就是那几个寥寥的著名例子。当然我承认，real analysis对于人的思维的升级和改造真的不是一个层次的，洞见力啊！

同样的，经济学里面那么多知识、模型，现在有多少又可以被我灵活的运用呢？我在不断的拷问自己。这也算是对于自己的一个考核指标吧：现在做的事情到底对未来有多大的意义。最多，也就是看看财经新闻的时候可以很不屑的对某些故意煽动情绪的分析嗤之以鼻，然后和别人纠结一下汇率、股市、房价等等其实我不怎么感冒的问题。不过，最近对我震撼最大的就是前几天去深圳玩的时候，跑到“深圳市博物馆”里面看了一下当年的深圳和改革开放前后的故事。真的，蛮有冲击力的，邓爷爷当年的洞见和魄力真的是让人钦佩万分！

这个时候才深深的意识到，上学的时候课本上一句“货币政策作用快、涉及面广”“财政政策作用慢、影响深”，即“一粗一细”之间的巨大差别。而现在，最大的争议，莫过于我国的出口退税政策吧。很简单的说，深圳的东西，出口到香港就可以享受17%的增值税返还，那么也就不足为奇为什么那么多深圳人周末去香港购物了。这么一个政策，我真的不知道它是在保护“出口加工贸易”这么一种产业模式，还是无力承受调整之后企业倒闭和失业增加的后果。可是，这个当年极大的带动了出口和就业的政策，还适应当前的国情么？我们的“内需”怎么可以承受这么一种不公平的价格杠杆呢？任何一个宏观模型，不都是以消费开始的么？没有市场价格下的消费，怎么可能有经济体的健康成长？

想到这里，觉得一个经济体的运作实在是有够复杂，一环扣一环的关系最终造就了终端产品的百花齐放。资本家会不惜一切代价的追求利益最大化，那么如果不能说服所有人、或者不存在一种可以让所有人信服的方法来维持平均分配主义，那么就应该按照市场的规则去玩这个游戏。财政政策永远是经济发展的擎肘啊。

古人云，读万卷书，行万里路。如果我应该珍惜什么，那就是在这个四处漂泊的工作中，尽可能多的体会各地的文化、经济和发展模式，然后形成自己的洞见和判断。现实总是让人意外的，以前在象牙塔确实是井底之蛙了。

最后附上几张图片：“世界之窗”里面的微缩版Park Guell和Barça的真实版 :)很有穿越感啊！
深圳版：


巴塞版：

Categories
事儿关经济

教育与科研精神

很少起这么大的一个题目，只是今天看到了一些“旧闻”，颇有种“有感而发”的情绪，所以就忍不住写下了这个题目。

文中提及的是OECD的PISA测试，我们先不管对于这个测试本身的争议，它大致反映了各国中学教育的水平。上海于2010年首次加入这个测试（共34个国家地区），结果自然“出人意料又在意料之中”：

China’s 15-year olds also took the test. They ranked 1st, 1st, and 1st.

猛地一看我还以为是发泄情绪呢，后来发现分别是三样测试的成绩。搜了一下关于pisa的新闻，关于这个结果的评论大多集中于这个测试到底可不可信。很多人觉得上海是一个特殊的样本，毕竟是中国经济最发达的地区。可是我却觉得不尽然——如果我们单单看成绩，尤其是高考成绩的话，上海大致是落后于全国平均水平的吧？我一直觉得上海好在素质教育，很多人多才多艺。所以很多人对于中国“应试教育”的批评，或许对上海不怎么适用。

中国重视教育，这个貌似是和东方文化一脉相承的，文中还有提及类似的香港、新加坡和日本的表现也都不俗。还有大家比较熟悉的就是中国的领导层几乎都是工程师或科学家出身，这怕是不太常见的——听说美国的政治家大都是律师出身。我无意争论这两者的好坏利弊，或许谁也无法短期内看得太清楚。只是这样的差异，倒也颇有意思。想想自己，弄得我这个学“人文学科”出身的倒是不知道自己应该如何立足了。

今天晚上和两位学长一起吃了一顿饭，顺便聊了很久很久。期间我提到一个模型，然后他们就开始帮我分析模型的事儿。分析了半天，就说到建模的精神的问题。我一直特别感激这学期碰到了Motta这么好的一位老师，非常强调直觉，而且他的直觉真的不是一般的好。有人说，建模建复杂了不是本事，建的简单才叫做本事。Motta就是有能力把复杂的模型简单化，取其精髓，把故事的来龙去脉讲清楚，让人一眼看透逻辑。这样的能力真的是让人惊叹——无论是面对同行学者、学生还是政府官员或产业界人士，他都能娓娓道来，大家都听得明白。这样的能力，着实难得！

我一直在想建模的事儿，一方面是写论文不得不做，另一方面也是对于自己经济学直觉的一次审视。这一年来，多多少少感觉自己的经济学直觉貌似有点降低了，不知道为什么。或许是这边太过于强调技术上的训练，多多少少总是在压迫自己做习题，所以很多时候就不知不觉的放松了对思维能力的训练。这次写论文，直觉不足的问题第一次耀眼的暴露在自己眼前。我一直是想让自己做到“无论是用数学还是文字，都是能把事情讲清楚的”，但是现在看来我的直觉还不足以支持我到这么高的一个境界。当然，我根本无法和Motta相比，毕竟他在竞争政策和反垄断领域浸淫了数十载，这些东西都看的通通透透了。我只是想follow自己的想法，然后表述一个自己脑海里面喜欢的故事。

突然间越来越体会到为什么说“社会科学家应该是越老越值钱”了，却记不得是何年何月听何人如此训教过了。对于一个社会，作为年轻人真的很难说理解它为什么这么运转，只有长期的浸没在里面，才能看得通透并知道如何融会贯通。去年的时候觉得，我还有许多东西要学，所以不能离开学校；现在看来，我还是有许多东西要学，只是学校里面未必能学到了。记得去年做决定离开学校的时候多多少少有些伤悲，毕竟喜欢了经济学这么久；现在却觉得这并不是完全的离开经济学，而是从另一个层次去体会经济学。这一年，给了我很好的一个机会肯定自己学习技术层面东西的能力，实分析和高宏彻底见证了技术层面的积淀；这一年，也深深让我体会到社会经验的不足，学校这个象牙塔可能不再适合我了。没有一项好的应用经济学研究是可以脱离真实生活直觉的。我一直有点固执的认为，就算是做理论经济学的研究，也是需要从应用经济学中获得的直觉来支撑的。连应用都做不好，又怎么可能完全架起来“空中楼阁”呢？