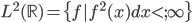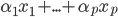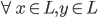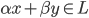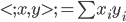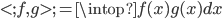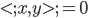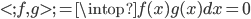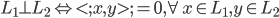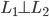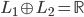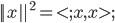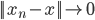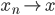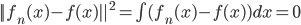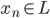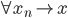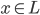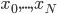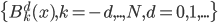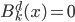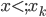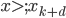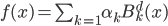题目用英文只是因为不知道怎么确切的用中文表达了。最近一直泡在数学里,很多思维大大的被改造了。不过很庆幸自己先学了经济学,否则就真的可能变成数学院某些“只有智商不见情商”的愣头学生们了。或者,万幸?
想起来这个题目,是突然间记起一直以来人们在争执的“经济学到底是不是硬科学”一问题。我不是如彭实戈之类的大家,无资格做什么评判,积累也远远不足。只是最近一直在努力的领悟泛函到底想说什么,一点浅薄的见识就是泛函中有一很重要的概念就是“列紧性”,也就是任意数列都存在收敛子列。这个东西可不得了,要知道类似于Banach之类的完备、赋范线性空间都是列紧的。那就很有研究的味道了~
那么,收敛意味着什么呢?当然,一方面是一个“有界”的概念,但是我个人觉得可能更重要的是一种“确定性”的思想。在压缩映像定理里面,我们证明了不动点的存在然后一堆方程就可以直接“迎刃而解”了。不动点这个东西推广到概率里面,那更是有意思的紧。不动,意味着方差为0;收敛,意味着均衡的存在。那么,一下子新古典经济学里面很多东西的存在就可以解释了。
最最简单的就是角谷不动点->纳什均衡->博弈论,一下子提供了一种看待问题的新的角度,是数学工具的更新让原来一些只能存在于思想意识中的概念得以规范的数理化,然后证明出来一系列漂亮的结论。
我窃以为,经济学中间最重要的概念就是“均衡”。经济学之所以超越其他社会科学而一枝独秀,最早就是从“一般均衡”理论的提出让其他学科难以望其项背。均衡的概念,贯穿与微观的供求分析中,贯穿于多人博弈的纳什均衡,贯穿于宏观经济增长模型的稳定,贯穿于动态市场结构的收敛均衡。所以说,均衡实在是在经济学中无处不在。而且这是一个和最优化并不矛盾的概念,有的时候两者甚至还是一致的,这一切都源于数学式子和经济学概念之间的完美映射。
记得当时去听彭老师讲座,他一开始就提出了各个时代各个地域哲学对于“不确定”和“确定”的定义。从这个角度来说,科学就是把原来不确定的事情先推导出来一个对应结果的概率,而后再进一步研究影响概率的条件以期最终能得到一种“确定性”。
从wiki对于science(科学)一词的定义,或许多多少少映证了我的理解:
Science (from the Latin scientia, meaning "knowledge") is, in its broadest sense, any systematic knowledge-base or prescriptive practice that is capable of resulting in a prediction or predictable type of outcome.
那么,为什么经济学总是难以堂而皇之的称作“科学”?是因为它的无法验证性?
总所周知,科学最大的意义就在于他的同胞兄弟:技术。科学是推动技术前进的力量,而技术是的的确确影响着我们的生活的。虽然学了那么多经济学,也受了多派对于经济增长观点的影响,但是我始终还是认为主导社会进步的是科学而不是制度。无论如何,科学的积累是需要时间的,也是需要天才的。虽然现代经济学总在关注制度,从微观的机制设计到宏观的经济体制和乃至法律,一切都是在比较着不同的制度,但是我还是窃以为这恰恰是一种经济学目前举步维艰的表现。
如果经济学确实是一门科学,那么它要做的就是从理论推导出应用,而后真正的去解决现实中的经济问题。上周在答Taiyun问的时候(参见:[cref %e7%ad%94taiyun%e9%97%ae3%ef%bc%9a%e7%bb%8f%e6%b5%8e%e5%ad%a6%e7%96%91%e9%9b%be%e9%87%8d%e9%87%8d%ef%bc%9f])曾经涉及经济学家与经济危机的问题。我的解释是经济学还是一门年轻的科学,我们远远还没有达到能去预测的地步,甚至连经济运行中的一些问题自己都看不清。所以在这样的意义上来说,虽然经济学在追求着均衡和确定性,但是还远远不够。
再回到数学。学了一些数学后,目前觉得数学最大的问题就是从“有限”到“无穷”的跨越。这个问题或许更应该说是一个哲学问题,但是它确实是在任何的数学领域中都有着深深的影响。为了绕过它,有了一系列的概念和假设,也有了一系列的约束。此类问题非吾等凡夫俗子可解,暂且搁置。只是在此问题上想通一点点,估计就成了叱咤风云的人物了。
然而经济学,却在此问题上差得远。其实某种程度上,或许有限与无穷、确定与不确定、收敛与发散等等都是一个哲学问题,只是不同层次上的表象而已。然而还未登上山峰,因此无法“一览众山小”,只能在山脚下妄自揣测。但愿不是井底之蛙,空谈无益。
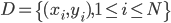 ,然后定义目标函数
,然后定义目标函数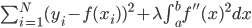 ,记为(1)
,记为(1)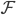 为函数族
为函数族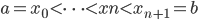 上的分段三次多项式(splines),且在首尾两段
上的分段三次多项式(splines),且在首尾两段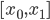 和
和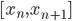 上是一次多项式,那么他一定有
上是一次多项式,那么他一定有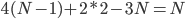 的自由度。
的自由度。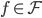 ,则当
,则当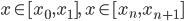 时,有
时,有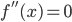 。
。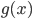 也是(1)式的解,则下面证明一定能找到
也是(1)式的解,则下面证明一定能找到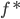 使得目标函数比
使得目标函数比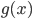 小,则
小,则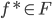 ,
,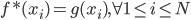 .
.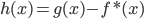 ,则
,则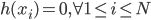
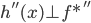 (两者内积为0),即
(两者内积为0),即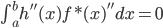 。
。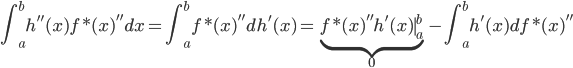

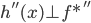 。
。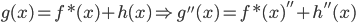 ,然后有
,然后有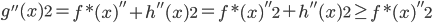 ,所以对于所有的g,我们都有其二阶导数的范数小于f的二阶导数的范数,故在(1)式中代入g总比代入f大(或者相等)。这样我们就把一个无限维的最优化问题变为了有限维。
,所以对于所有的g,我们都有其二阶导数的范数小于f的二阶导数的范数,故在(1)式中代入g总比代入f大(或者相等)。这样我们就把一个无限维的最优化问题变为了有限维。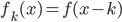
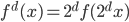
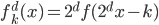 。由此,对于每个
。由此,对于每个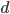 ,我们可以定义一个函数族
,我们可以定义一个函数族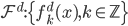 ,写成矩阵形式就是
,写成矩阵形式就是
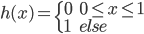 。
。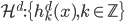 ,
,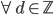 。这样我们每个
。这样我们每个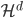 为一组(胖瘦一样)。
为一组(胖瘦一样)。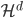 是
是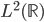 平方可积函数的一个正交基,即对于任意的
平方可积函数的一个正交基,即对于任意的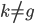 ,有
,有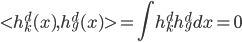 。
。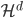 张成的闭子空间逐渐增大,且
张成的闭子空间逐渐增大,且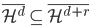 。这样,d比较小的函数一定能用d比较大的函数(正交基)来表示,比如
。这样,d比较小的函数一定能用d比较大的函数(正交基)来表示,比如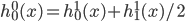 。直观的理解就是,d越大,分辨率越高。
。直观的理解就是,d越大,分辨率越高。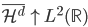
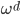 ,使
,使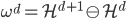 ,或者
,或者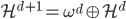 。
。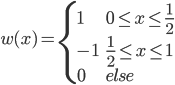 ,然后
,然后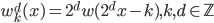 。
。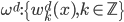 ,
,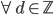 ,则
,则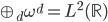 亦为完备基,且
亦为完备基,且 ,如果
,如果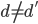 。也就是说,
。也就是说, 和
和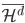 之间的空间随着d的增加,彼此正交,且所有的叠起来之后亦为完备空间。
之间的空间随着d的增加,彼此正交,且所有的叠起来之后亦为完备空间。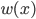 为子波(mother)而
为子波(mother)而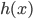 为father函数。注意,这里Hoar函数非连续。
为father函数。注意,这里Hoar函数非连续。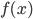 为father函数,然后定义
为father函数,然后定义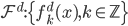 ,满足
,满足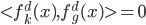 (正交),且
(正交),且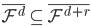 (增长),
(增长),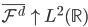 (完备)。
(完备)。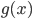 满足
满足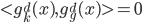 (同层次内正交)、
(同层次内正交)、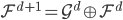 (相邻层次正交补)和
(相邻层次正交补)和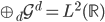 完备。
完备。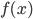 和
和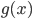 到底存不存在呢?实证结论是存在,而且很多,不过坏消息是他们的形式都不算简单。
到底存不存在呢?实证结论是存在,而且很多,不过坏消息是他们的形式都不算简单。