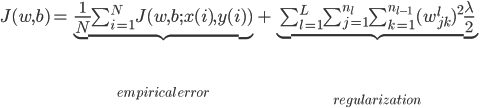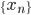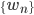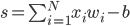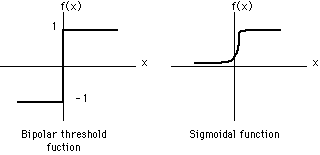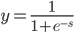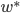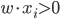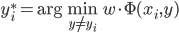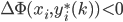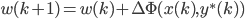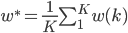年纪越大,越不想写什么年终总结之类的,感觉记住的就记住了,记不住的就任其遗忘就好了,不必刻意的一条条的列出来。2018年的最后一天,五点钟就会落下的太阳。日落前的两个小时,还算闲暇,就趁机写一些我还记得住的一些事情。
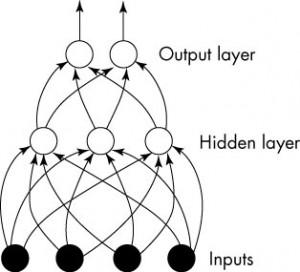
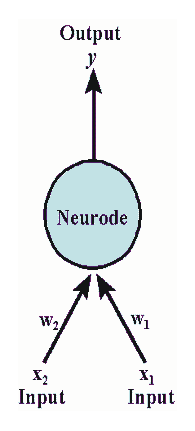
潮流:机器学习和深度学习
身处硅谷,就算再不关心机器学习,周围的人也总是会叫嚷着,于是乎被动学习了。我一直属于不怎么刻意去关心热点的人,感觉深度学习这几年热得发烫,却不知道到底烫在哪里。打开科技新闻,要么是无人车,要么是视频换脸,感觉视觉识别已经越来越发达了。打开购物网站,各种智能家居应用层出不穷,语音识别自然是其中最重要的技术支撑。
十二月,多少得到一点闲暇时间,有意识的去扫了一眼这个领域最近的一些论文和twitter上大佬们的辩论。有朋友戏称大多数人的深度学习就是调参,这么想想更像是一种工匠精神的极致发挥。每一项工业用品,譬如飞机,都是一点一点调出来的零件和参数组合。你说所有的一定是最佳么,未必,但非最优解也有可能给出很稳定的表现。这么想想,看看深度学习层出不穷的各种领域和数据集上实践的论文,也是人们智慧和探索的结晶。
只是理论的进展呢?没有理论的长远发展和支撑,应用的突破大概也可以看到天花板。后面有时间打算去看看深度学习的理论,然而不止一个人打击我说,深度学习并没有什么理论。我想,大概还是会有一些的吧,只是还没有坚实到一个成熟的理论体系里面。四五年前,我经常笑谈说,深度学习会不会是下一个微积分?大家先用着,然后实践倒逼理论臻于完美。好几个朋友笑笑,不了了之。不知不觉好几年又过去了,深度学习居然还是那么热,但理论的进展却没有想象中的那么快。理论如果真的没有进展,那么深度学习会不会又一次陷入神经网络曾经的绝境呢?
隔岸观火,好在我有的是耐心。硅谷聚集了一群最聪明的大脑,就算只是工匠般的推敲,一点点开凿出道路,也足以让人钦佩。只是世间万事,最终逃不过客观规律。只是不知道需要多久,这一代人才可以突破迷雾,探得镜中花。
旅行:疲惫和兴奋
每年年末我好像都会总结一下一年中去过的地方,算是一个小小的纪念。去年走过了五大洲,而今年频率更高。下半年因为工作的缘故,几乎是每个月出境一趟,却只是在北美和欧洲之间穿梭,除了回国一次。到了一定程度之后,已经比较难找到下一个说走就走的旅行目的地了。看遍世间繁华,大同小异,殊途同归。
当疲惫到连去欧洲都不用心打包,缺什么现场买什么,我想我对国际旅行的心里疲倦已经到了一个不可挽回的程度了。一个人旅行那种随意和不确定性,已经不能让我如往年那样兴奋了。
工作:方向和勇敢
工作永远都是起起伏伏的。顺的时候,项目进展神速,没什么需要过度担心的。不顺的时候,皱着眉头想了许久,才得以找寻到几个可以修修补补的地方。时间久了,幺蛾子见多了,也就见怪不怪了。
工作上最难的永远不是学习不知道的知识,也不是越做越熟少出纰漏。解决一个问题固然可能需要一些时间,但总归是能找到办法的。而寻找下一个突破点,才是让人彻夜难寐的事情。相比于前进的方向,具体的零零碎碎的问题就显得不那么重要了。很多事情虽说是殊途同归,但也得大致方向一致。
2018,有一些突破,尝试了退一步海阔天空的清爽。曾经有一段时间的迷茫,因为看到周围少数几个人坚定地向着梦想前进的果决,相比而言自己的犹豫不决显得格格不入。后面追问着自己一些本质的问题,比如什么事情可以给我持续的快乐,我又想成为什么样的人,或者不想成为什么样的人。这些问题渐渐的明晰起来,然后只是如何寻找到前进的道路而已。还算有一个稳定的平台支撑着,那么就不妨承担一些风险,试错,徘徊前行。
勇敢着,很多事情回头看,当时的结果已经并不重要。各种经历,最终造就了独特的人生。
其他
生活上,各种莫名其妙的技能在增加。学会一些意料之外的技能,解决一些生活实际问题,其实还蛮好玩的。
体重意料之外的,降到了这么多年的最低点。顺手量了量三围,虽说不用靠三围赚钱养活自己,但看着这些数字指标还是蛮开心的。
文字方面,博客更新寥寥无几。偶尔会在手机上写一些随感,翻了翻英文居然不比中文少。衷肠苦诉,情绪的波动和管理越来越成熟,却少了几分跌宕起伏的兴奋。