呃，我觉得我的笔记稍稍有点混乱了...这周讲的依旧是线性分类器，logit为主。anyway，大家将就着看吧。
logistic regression
首先我们考虑最一般的，有K种分类的场合。依旧，我们用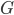
来代替
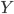作为观测到的分类结果，那么则有：
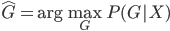为最优的预测结果。这里我们希望找到一种线性的形式，还需要使用一些单调变换保证预测值在
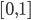之间。因此，我们对于每个分类
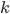，假设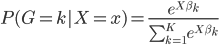
进一步的，我们取任意类K作为对照组，且各组相加概率之和必为1，所以有：
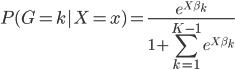且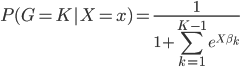
所以，最终得到两组之间的概率比值为：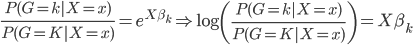
最后求解的时候，就是直接用最大似然准则，来求解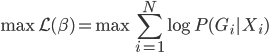
这个最大似然函数计算起来比较麻烦，通常很多是数值解。下面以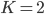
为例，来展示求解过程。
首先我们这个时候有两类，不妨记作1和0，则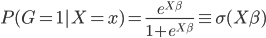
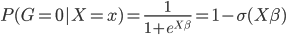则它的对数似然函数:
然后我们求导可得：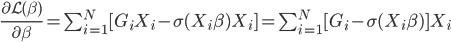
之后可以用牛顿法迭代求数值解：
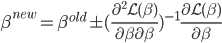
其中二阶导数部分可以化简为：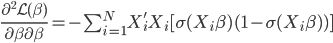
记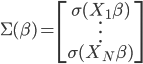
且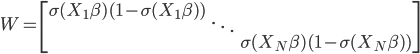
则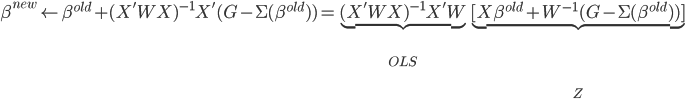
经过简化之后，这里相当于加权的最小二乘法，目标函数为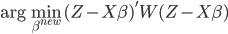
所以整个算法可以写作：
0. 令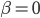
或任意起始值
1. 计算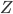
矩阵.
2. 新的
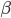为.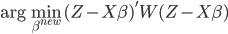
3. 重复1，2步直至收敛。
这类方法成为IRLS（不断重写的加权最小二乘法）。
LDA和logit选择
其实也没什么定论，两者均为线性，只是一般我们认为LDA需要假设联合正态且方差相等，比较强；而logit假设没有这么强，相比而言更稳定。
perceptional分类器
perceptional分类器是一类相对简单的分类算法，以两类场合为例。为了方便起见，我们假设两类为1和-1，则目标是找出一条直线可以完全分割出来两群点。这里转化成数学的语言，就是找到W使得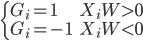
或者简化为：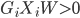
算法也很简单：
1. 给定任意的W值，比如0. 如果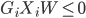
，出错。
2. 令新的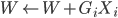
，重复第一步。
这里可证一个定理：如果原数据集是线性可分的（即W存在），那么在有限步内perceptional算法收敛。其实从第二步可以看出，这样的改进总是趋近于目标的：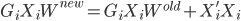
，一定是在逐步增加的。
同样的算法推广到多累场合，我们就需要引入特征向量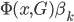
，使得条件概率
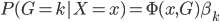。这样我们的目标就是找到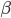使得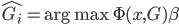
同样的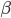，从0开始，当
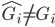时，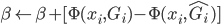
，直至收敛。
不过有意思的是，实践证明，最后使用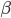训练过程中的
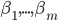的平均值效果会更好，而不是最终的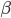值。
--------笔记结束，废话开始--------
到这里，分类器吴老师已经介绍了三类：LDA，Logit和perceptional。其实我一直觉得比较好玩的是分类器和聚类方法的对比——虽然一个是有监督，一个是无监督的学习，不过有的时候我们就算有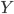的观测值也不一定直接就去用——聚类方法某种程度上显得更加自然一些。这也是大家把模型与实际业务相结合起来的成果吧，总要更符合业务上的直觉才可以。是自然的展现群落的形态，还是给定一些条条框框只是去预测？实践中真的是，都去试试才知道那种更符合一个具体案例的需求。这也是在industry玩的比较开心的缘故，没有那么多条条框框，没有那么多“约定俗成“的规矩，需要自己去一步步挖掘这些算法的用武之地。看着一个个自己熟悉或者陌生的模型被逐渐的改造和应用，也是一件蛮开心的事情呢。