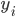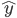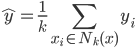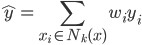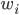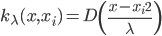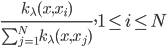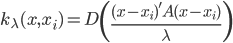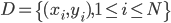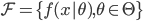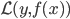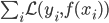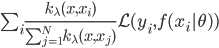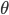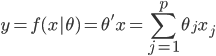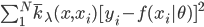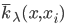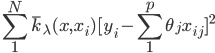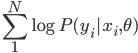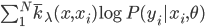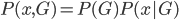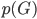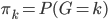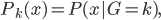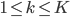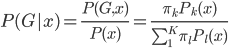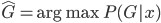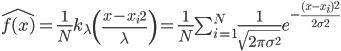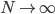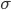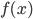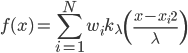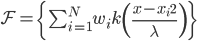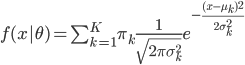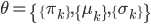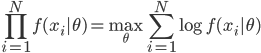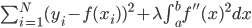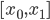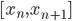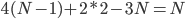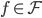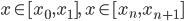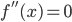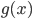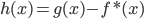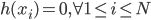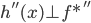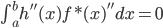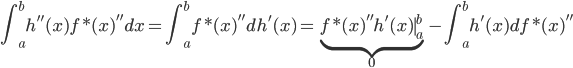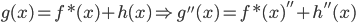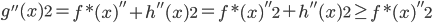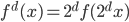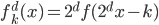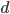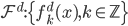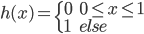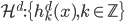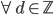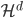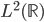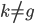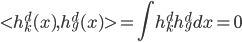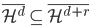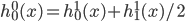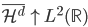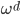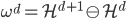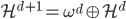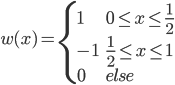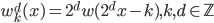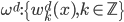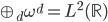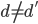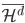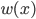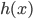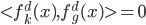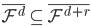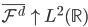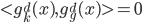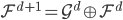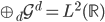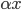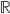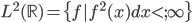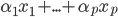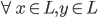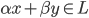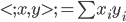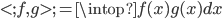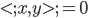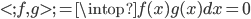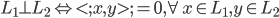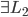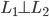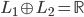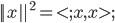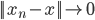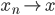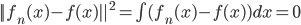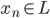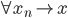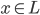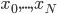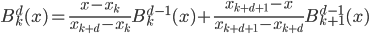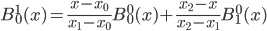降维
降维完全属于unsupervised learning了,即给定数据集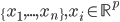 ,我们希望降到q维的
,我们希望降到q维的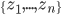 。从这个角度来讲,降维和聚类还是有相通之处的,都是对于特征的提取。只是一个从行的角度出发,一个对列操作的感觉。
。从这个角度来讲,降维和聚类还是有相通之处的,都是对于特征的提取。只是一个从行的角度出发,一个对列操作的感觉。
PCA(主成分分析,Principle Component Analysis)
个人觉得这也是起名字起的比较好的模型之一...乍一听起来很有用的感觉 -_-||
1. 求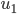 ,
,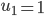 使得
使得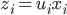 ,且
,且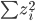 最大。
最大。
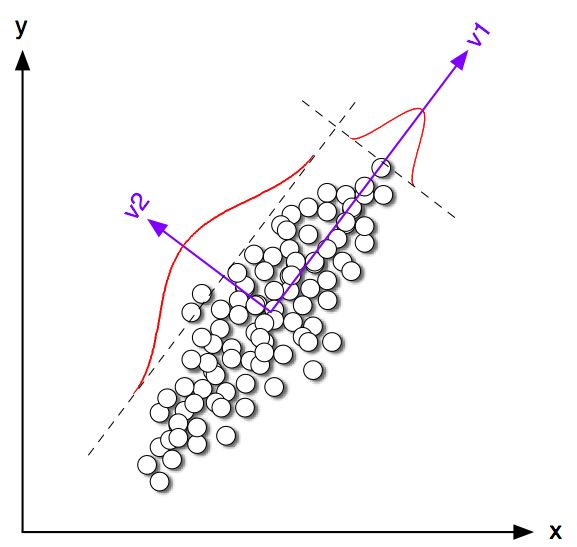
直觉上来讲,就是想寻找一个主方向。
这样,求解问题为:
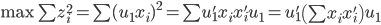 。所以我们只需要求一阶导数
。所以我们只需要求一阶导数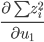 即可。
即可。
设A为对称矩阵,则存在正交阵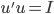 使得
使得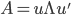 ,其中
,其中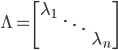 为A的特征值矩阵,故
为A的特征值矩阵,故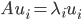 (列向量为特征向量)。不失一般性,我们可以排序使得
(列向量为特征向量)。不失一般性,我们可以排序使得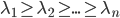 (从大到小排序)。
(从大到小排序)。
最大特征值: 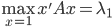
同时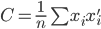 为x的相关矩阵,
为x的相关矩阵,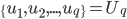 ,从而
,从而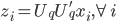
2. 找到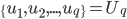 (q维的子空间)
(q维的子空间)
将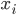 投影到该q维空间,这样
投影到该q维空间,这样 ,且
,且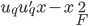 最小。
最小。
A矩阵的范数: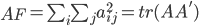
tr表示矩阵的迹(对角线元素和)。
则上述问题等价于,求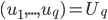 使得
使得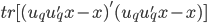 最小。
最小。
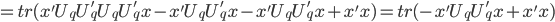 最小。
最小。
即使得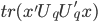 最大(注意没有负号)。
最大(注意没有负号)。
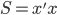 称为数据的相似矩阵
称为数据的相似矩阵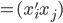 。
。
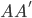 和
和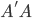 均为对称阵,且两个阵有相同的特征值。记
均为对称阵,且两个阵有相同的特征值。记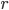 为A的秩,AA'的特征向量
为A的秩,AA'的特征向量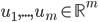 ,A'A的特征向量
,A'A的特征向量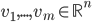 ,则
,则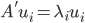 ,
,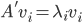 。做奇异值分解,则
。做奇异值分解,则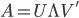 .
.
由此,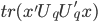 求得的和前述结果等价。
求得的和前述结果等价。
回到PCA。如果降维后需要重构,则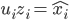 ,解
,解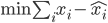 即可。
即可。
3. 对偶PCA。如果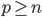 即数据非常高的时候,可以转置后再做。
即数据非常高的时候,可以转置后再做。
4. KPCA (kernel)PCA也可以先用核函数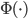 ,即实现非线性的降维。需要注意,降维的过程需要保持可逆。
,即实现非线性的降维。需要注意,降维的过程需要保持可逆。
---------------
PS. PCA不适合解决overfitting的问题。如果需要解决,加regularization项。