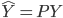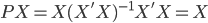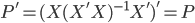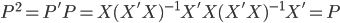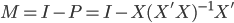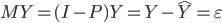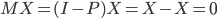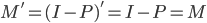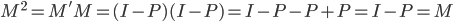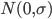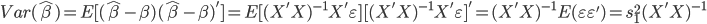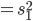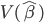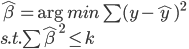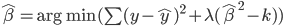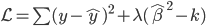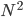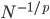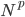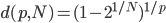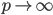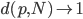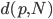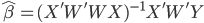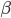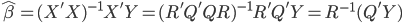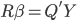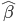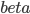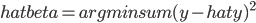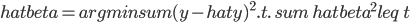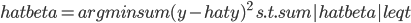主要是最近看到了一系列相似的文章,就忍不住说说这一系列文章的好玩之处。这一系列的文章主要是用假的CV来投简历,然后根据HR的电面反馈来探究CV中不同因素对于求职者的影响。当然一开始最关注的就是是不是就业市场中间有性别歧视——即给定两个能力一模一样工作经历也类似的,一男一女,难道女生会因为性别原因而遭受歧视么?
鼓捣出来这种折磨我们亲爱的各大企业HR的方法的就是芝加哥大学的Bertrand, Marianne和Mullainathan, Sendhil (其中后者已经转战到哈佛去了),以及他们那篇著名的AER论文:
Bertrand, Marianne and Mullainathan, Sendhil (2002). "Are Emily and Jane More Employable than Lakisha and Jamal? A Field Experiment on Labor Market Discrimination,". American Economic Review94 (4): 991. doi:10.1257/0002828042002561.
哎,可能开始接触计量经济学或者劳动经济学的,这都是逃不掉的一篇paper吧。idea 真的是很简单:搞一堆相似的简历,只是姓名和性别有所不同,然后投到各大公司,追踪反馈。这样就回答了那个本来看起来无法回答的问题:我们观察到的女性平均工资低于男性,是因为性别歧视还是因为女性的能力较男性差一些?在这里相似的简历代表求职者有着相似的能力,所以能力那个因素就变得可控了,只需要探究性别上的差别就可以了。这样就把一个本来没法做随机试验的内生性问题,巧妙的用另外一种实验设计来稍稍回答了(毕竟只是电面通知,而不是最终的录取。CV容易fake,面试就没办法了)。
结果这篇文章一出,因其idea简单、可行性好、成本低(找几个学生发发邮件就可以了),一下子受到很多被折磨经久的经济学研究者的青睐,然后类似的paper便如雨后春笋般的爆发——不仅仅是美国公司的HR开始遭殃,瞬间各国有着发paper需求的劳动经济学家们开始纷纷效仿、一拥而上,先是席卷欧洲大陆,然后亚洲自然也难以逃掉。嗯,于是就看到下面这些paper:
- 西班牙:Albert, Rocío, Lorenzo Escot Mangas, and José Andrés Fernández Cornejo. "A field experiment to study sex and age discrimination in selection processes for staff recruitment in the Spanish labor market." Papeles de trabajo del Instituto de Estudios Fiscales. Serie economía 20 (2008): 3-46.
-
澳大利亚:Booth, Alison, and Andrew Leigh. "Do employers discriminate by gender? A field experiment in female-dominated occupations." Economics Letters 107, no. 2 (2010): 236-238.
- 英国:Riach, Peter A., and Judith Rich. "An experimental investigation of sexual discrimination in hiring in the English labor market." Advances in Economic Analysis & Policy 6, no. 2 (2006): 1-20.
- 中国:Zhou, Xiangyi, Jie Zhang, and Xuetao Song. "Gender Discrimination in Hiring*: Evidence from 19,130 Resumes in China."
- 意大利:Patacchini, Eleonora, CEPR Giuseppe Ragusa, and LUISS Guido Carli. Unexplored Dimensions of Discrimination in Europe: Homosexuality and Physical Appearance. No. 9179. CEPR Discussion Papers, 2012.
- “Duration Dependence and Labor Market Conditions: Theory and Evidence from a Field Experiment” (with Fabian Lange and Matthew J. Notowidigdo). Quarterly Journal of Economics, Forthcoming.
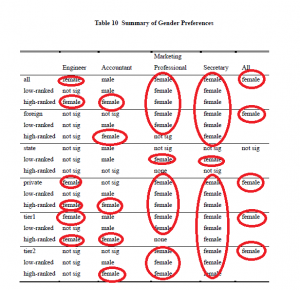
其他的我暂时没有搜了,已然觉得足够了。最后上一张中国劳动力市场的结果——怪不得现在研究劳动力市场都要把中国作为一个outlier呢,华夏女性实在是太强了!