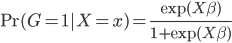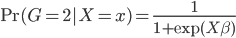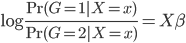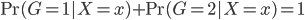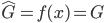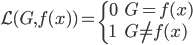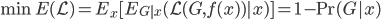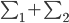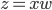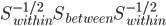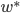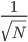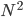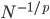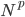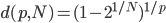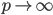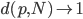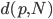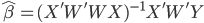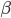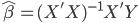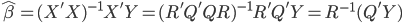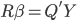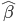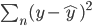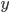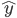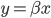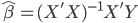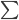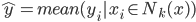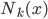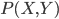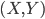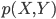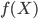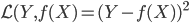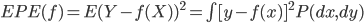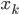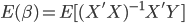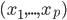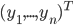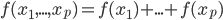照例文章第一段跑题,先附上个段子(转载的哦~):
I hate CS people. They don't know linear algebra but want to teach projective geometry. They don't know any probability but want to use graphical models. They don't understand stats at all but still do machine learning like crazy.
喵,最近被问了好几次machine learning 和statistical learning的区别在哪里,我觉得大致如上吧。这也是为什么,对后面这个词我的好感稍稍好于前面那个的原因...科学总是有意义的嘛,不能总是依靠强力乱猜是不是嘛。
免责声明:以下个人见解部分局限于我个人的见识和思考范围,不适用于所有场景。请大家弃糟粕取精华,不可一言全信之。
-------------笔记+随想开始------------
高维空间问题
这一段主要是说大名鼎鼎的"维数灾难"。我们都知道有两个数字决定着OLS中X矩阵的大小,这就是 观测数目N 和观测变量的个数p 。一般说来,我们都喜欢N比较大,这样可以很容易的应用大数定律什么的。然而对于p,却是既爱又恨—我们当然喜欢可以观察到个体的很多个特征,但是所谓"乱花渐欲迷人眼",特征越多噪音也越多,搞不好预测的时候就会有麻烦(关于变量的选择问题,应该是下一节课的内容。心急的可以先看看我以前的一篇自学笔记)。
为什么维数增多的时候会麻烦呢?这里主要是随着维数增多带来的高维空间数据稀疏化问题。简单地说:
- p=1,则单位球(简化为正值的情况)变为一条[0,1]之间的直线。如果我们有N个点,则在均匀分布的情况下,两点之间的距离为1/N。其实平均分布和完全随机分布的两两点之间平均距离这个概念大致是等价的,大家可稍微想象一下这个过程。
- p=2,单位球则是边长为1的正方形,如果还是只有N个点 ,则两点之间的平均距离为
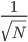 。换言之,如果我们还想维持两点之间平均距离为1/N,那么则需
。换言之,如果我们还想维持两点之间平均距离为1/N,那么则需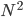 个点。
个点。
- 以此类题,在p维空间,N个点两两之间的平均距离为
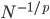 ,或者需要
,或者需要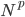 个点来维持1/N的平均距离。
个点来维持1/N的平均距离。
由此可见,高维空间使得数据变得更加稀疏。这里有一个重要的定理:N个点在p为单位球内随机分布,则随着p的增大,这些点会越来越远离单位球的中心,转而往外缘分散。这个定理源于各点距单位球中心距离的中间值计算公式:
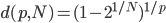
当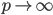 时,
时,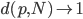 。(很显然,当N变大时,这个距离趋近于0。直观的理解就是,想象我们有一堆气体分子,p变大使得空间变大,所以这些分子开始远离彼此;而N变大意味着有更多气体分子进来,所以两两之间难免更挤一些。看过《三体》的,大概会觉得这个很熟悉的感觉吧...四维空间下的"水滴"再也不完美的无懈可击,而一张一维的纸片就毁灭了整个地球呢。)
。(很显然,当N变大时,这个距离趋近于0。直观的理解就是,想象我们有一堆气体分子,p变大使得空间变大,所以这些分子开始远离彼此;而N变大意味着有更多气体分子进来,所以两两之间难免更挤一些。看过《三体》的,大概会觉得这个很熟悉的感觉吧...四维空间下的"水滴"再也不完美的无懈可击,而一张一维的纸片就毁灭了整个地球呢。)
这个距离公式的推导就暂时不写了,好麻烦...大致是利用了各个点独立同分布的特性(完全随机情况下),把median距离变为以1/2概率大于中位数的概率集合公式,再进一步展开为单点距离累乘公式。
比如当p=10, N=500的时候,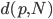 约为0.52,也就意味着有一半多的点离中心的距离大于1/2。
约为0.52,也就意味着有一半多的点离中心的距离大于1/2。
高维问题为什么是问题呢?回顾一下K近邻算法,我们用x的邻居来代替x,这样就希望他的邻居们不要离他太远。显然高维空间使得点和点之间越来越远。所以说,knn更适合小p大N即低维多观测量的情况,而在高维空间下可能会变得很麻烦。
这样,statistical learning的主要两个问题就总结完了:
- 过拟合:为了控制预测误差,我们要选择适合的函数类。
- 高维空间:随着维数的增多,我们面临着维数灾难。这对很多算法都有波及,主要体现在高维数据稀疏化。
回归的线性方法
这里主要是一些linear regression的东西,作为被计量经济学折磨了这么多年的孩子,我表示很淡定...此外还加上我们俗称的generalized linear models,即GLM。一些线性变换而已,无伤大雅。
这里一定要强调的是,在这里我们亲爱的X居然不是随机变量!多大的一个坑啊,我就华丽丽的掉下去了还问老师为什么无偏性不需要假设均值独立什么的... X不是随机变量意味着什么呢?X是人为设定或者决定的,比如我一天浇200 ml 或者500 ml水,然后看对于植物生长的影响。当时我真的是想"一口老血喷出来",这也太舒服了吧!要知道大多数情况下X也是随机变量哇,比如身高体重什么的。如果它不是随机变量而只有扰动项是独立的随机变量的话,整个计量经济学怕是要删掉好多篇幅了呢。我想说的只有,这群搞statistical learning的好幸福...
X不是随机变量的时候,为了满足无偏性的假设,只需要扰动项不相关且期望方差存在就可以了。期望不为0不要紧,回归的时候放进去常数项就可以了。
此外,对于任意一个正定阵W,我们都可以直接在回归方程两边乘以W,从而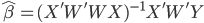 。也就是说,我们可以给X进行加权处理,加权矩阵W之后可以进行新的OLS估计,且可能会有对应的优良性质。加权最小二乘法我就不在这里复习了,学过计量的应该很熟悉,比如处理异方差什么的。
。也就是说,我们可以给X进行加权处理,加权矩阵W之后可以进行新的OLS估计,且可能会有对应的优良性质。加权最小二乘法我就不在这里复习了,学过计量的应该很熟悉,比如处理异方差什么的。
再就是我们可以给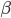 加上一些约束条件,这样的话最小化问题后面就可以简单的使用拉格朗日乘子法来解。
加上一些约束条件,这样的话最小化问题后面就可以简单的使用拉格朗日乘子法来解。
这次的收获之一就是OLS估计量的计算。在实践中,我们计算OLS估计值并不是直接使用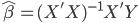 ,而是会事先进行QR分解(利用特征值来算)。即,我们把X分解为化为正交(酉)矩阵Q与实(复)上三角矩阵R的乘积。这样一来,
,而是会事先进行QR分解(利用特征值来算)。即,我们把X分解为化为正交(酉)矩阵Q与实(复)上三角矩阵R的乘积。这样一来,
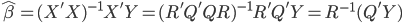
这样可解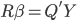 ,计算时候的稳定性比直接求逆矩阵来的好很多,因为计算机必竟有数字长度的限制,各种位数带来的精度损耗最后会累积到估计量上。
,计算时候的稳定性比直接求逆矩阵来的好很多,因为计算机必竟有数字长度的限制,各种位数带来的精度损耗最后会累积到估计量上。
最后就是高斯-马尔科夫定理,就是我们常说的BLUE估计量。我就直接拷贝这个定理了:
在误差零均值,同方差,且互不相关的线性回归模型中,回归系数的最佳无偏线性估计(BLUE)就是最小方差估计。一般而言,任何回归系数的线性组合的最佳无偏线性估计就是它的最小方差估计。在这个线性回归模型中,误差既不需要假定正态分布,也不需要假定独立(但是需要不相关这个更弱的条件),还不需要假定同分布
进一步的,如果假设扰动项服从正态分布,比如白噪声,那么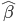 的估计值也服从正态分布,y的预测值也服从正态分布,因此可以直接做一系列基于正态分布的假设检验。特别的,在大样本情况下,就算扰动项不是正态分布,我们也还是可以利用大数定律和中心极限定理...事实上一般也是这么做的。
的估计值也服从正态分布,y的预测值也服从正态分布,因此可以直接做一系列基于正态分布的假设检验。特别的,在大样本情况下,就算扰动项不是正态分布,我们也还是可以利用大数定律和中心极限定理...事实上一般也是这么做的。
本节课到此结束。老师没有一一推导无偏性最小方差这些性质,我倒是觉得对回归方法感兴趣的还是直接去看计量经济学吧。这东西水还是蛮深的。
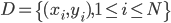 ,然后定义目标函数
,然后定义目标函数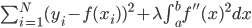 ,记为(1)
,记为(1)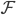 为函数族
为函数族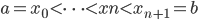 上的分段三次多项式(splines),且在首尾两段
上的分段三次多项式(splines),且在首尾两段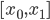 和
和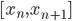 上是一次多项式,那么他一定有
上是一次多项式,那么他一定有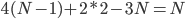 的自由度。
的自由度。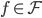 ,则当
,则当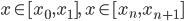 时,有
时,有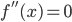 。
。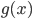 也是(1)式的解,则下面证明一定能找到
也是(1)式的解,则下面证明一定能找到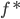 使得目标函数比
使得目标函数比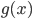 小,则
小,则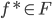 ,
,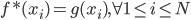 .
.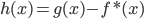 ,则
,则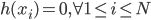
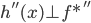 (两者内积为0),即
(两者内积为0),即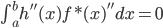 。
。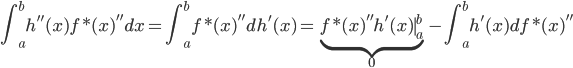

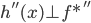 。
。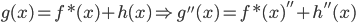 ,然后有
,然后有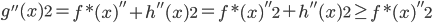 ,所以对于所有的g,我们都有其二阶导数的范数小于f的二阶导数的范数,故在(1)式中代入g总比代入f大(或者相等)。这样我们就把一个无限维的最优化问题变为了有限维。
,所以对于所有的g,我们都有其二阶导数的范数小于f的二阶导数的范数,故在(1)式中代入g总比代入f大(或者相等)。这样我们就把一个无限维的最优化问题变为了有限维。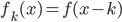
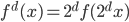
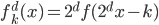 。由此,对于每个
。由此,对于每个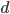 ,我们可以定义一个函数族
,我们可以定义一个函数族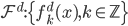 ,写成矩阵形式就是
,写成矩阵形式就是
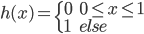 。
。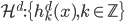 ,
,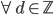 。这样我们每个
。这样我们每个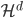 为一组(胖瘦一样)。
为一组(胖瘦一样)。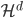 是
是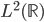 平方可积函数的一个正交基,即对于任意的
平方可积函数的一个正交基,即对于任意的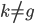 ,有
,有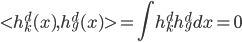 。
。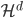 张成的闭子空间逐渐增大,且
张成的闭子空间逐渐增大,且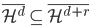 。这样,d比较小的函数一定能用d比较大的函数(正交基)来表示,比如
。这样,d比较小的函数一定能用d比较大的函数(正交基)来表示,比如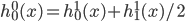 。直观的理解就是,d越大,分辨率越高。
。直观的理解就是,d越大,分辨率越高。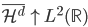
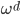 ,使
,使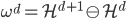 ,或者
,或者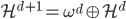 。
。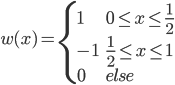 ,然后
,然后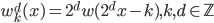 。
。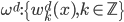 ,
,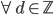 ,则
,则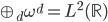 亦为完备基,且
亦为完备基,且 ,如果
,如果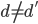 。也就是说,
。也就是说, 和
和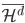 之间的空间随着d的增加,彼此正交,且所有的叠起来之后亦为完备空间。
之间的空间随着d的增加,彼此正交,且所有的叠起来之后亦为完备空间。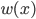 为子波(mother)而
为子波(mother)而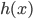 为father函数。注意,这里Hoar函数非连续。
为father函数。注意,这里Hoar函数非连续。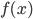 为father函数,然后定义
为father函数,然后定义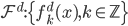 ,满足
,满足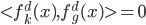 (正交),且
(正交),且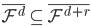 (增长),
(增长),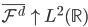 (完备)。
(完备)。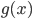 满足
满足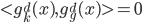 (同层次内正交)、
(同层次内正交)、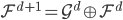 (相邻层次正交补)和
(相邻层次正交补)和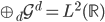 完备。
完备。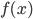 和
和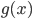 到底存不存在呢?实证结论是存在,而且很多,不过坏消息是他们的形式都不算简单。
到底存不存在呢?实证结论是存在,而且很多,不过坏消息是他们的形式都不算简单。