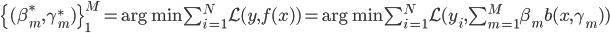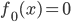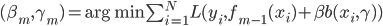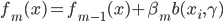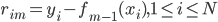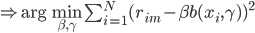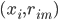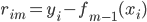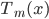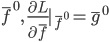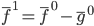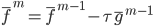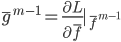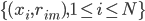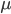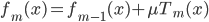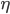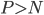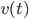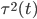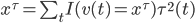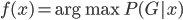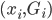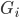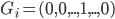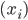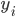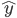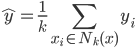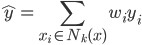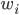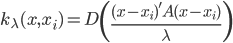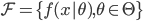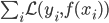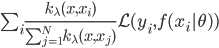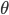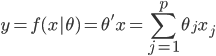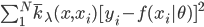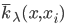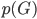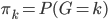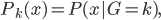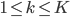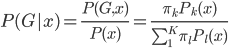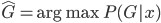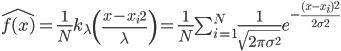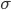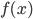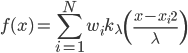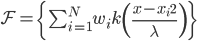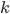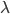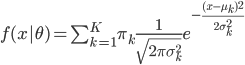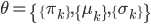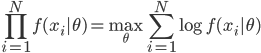笔记(二十二)需要等我找到上一本笔记本再说,暂时不知道扔到哪里去了...汗。届时补上。
这一章主要是讲的原型方法(prototype)和最近邻(KNN)。相对而言直觉更强,公式没那么复杂。
--------------------------笔记开始-------------------
1. 原型方法
1) 1-NN 最近邻居方法
最极端的情况:只找到最近的一位邻居。
数据集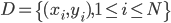 ,输入
,输入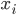 ,在
,在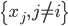 中找到与
中找到与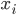 最近的邻居
最近的邻居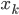 ,输出
,输出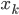 对应的类标记
对应的类标记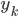 。
。
2) 类中心的方法
类中心: 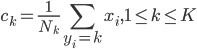 ,相当于对于一群有着同样类标记的点,对x取平均。
,相当于对于一群有着同样类标记的点,对x取平均。
输入: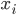 ,而后在所有类中心中与其最近的类中心
,而后在所有类中心中与其最近的类中心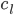 。
。
输出: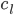 对应的类标记。
对应的类标记。
3) 对每个类可计算若干个“中心”(称之为原型或者样板,比如在每类中做聚类)。
输入: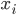 ,而后在所有类中心中与其最近的类中心
,而后在所有类中心中与其最近的类中心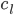 。
。
输出: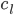 对应的类标记。
对应的类标记。
4) K-NN方法
输入: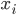 ,在
,在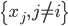 中找到与
中找到与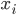 最近的K个邻居。
最近的K个邻居。
输出: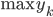 (最多的那一类,从众原则的感觉)。
(最多的那一类,从众原则的感觉)。
由于这一类方法都比较懒,所以称之为lazy learning methods.
2. K-NN方法的错误率(渐近性质)
1) 结果
设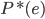 为Bayes分类器的错误概率(最优分类器);
为Bayes分类器的错误概率(最优分类器);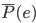 为1-NN分类器的错误概率。
为1-NN分类器的错误概率。
则有:当样本数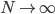 时,
时,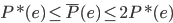 。接下来会证明这个优良的性质。
。接下来会证明这个优良的性质。
2) 分类问题
给定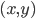 ,则
,则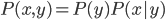 。
。
这里我们称 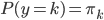 为先验分布,
为先验分布,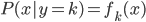 为类分布。从而
为类分布。从而
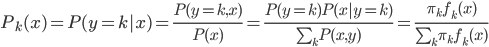 ,称之为后验概率。
,称之为后验概率。
3) Bayes分类器
x对应的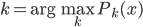 ,即使得后验概率最大的k。
,即使得后验概率最大的k。
所以,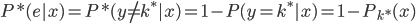 ,从
,从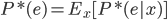 。
。
4) 1-NN分类器
1-NN输出的是离x最近的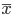 对应的
对应的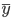 ,则
,则
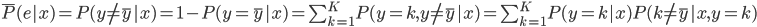 。
。
由于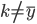 只限训练集,而
只限训练集,而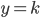 那部分只跟测试集有关,所以由独立性我们可以拆分为:
那部分只跟测试集有关,所以由独立性我们可以拆分为:
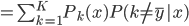 ,则当
,则当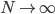 时,
时, ,
,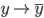 ,上面一项可以收敛为
,上面一项可以收敛为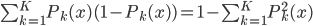 ,为后验概率(条件误差)。
,为后验概率(条件误差)。
5)由于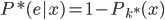 ,设
,设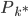 为所有
为所有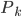 中最大的,则
中最大的,则
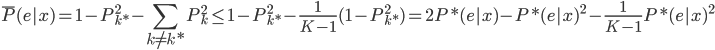
6)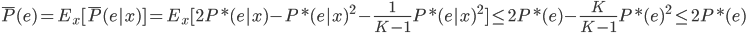 。得证。
。得证。
下一章会讲到聚类,然后就是降维了。