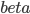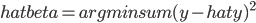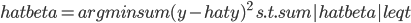算了,还是“一心只读圣贤书”吧。我觉得保险公司应该开发一个新险种:高铁动车险。你看我们坐汽车坐飞机都可以有保险买的,怎么坐火车的时候从来都没有这个选项?飞机的旅行保险貌似是细致到各种可能出现的事端,比如“晚点”、“取消”,那么高铁保险也可以以“停电”“雷击”“脱轨”等等名义来帮助消费者分担风险。最近看新闻看多了,弄得我这个在欧洲这么一个航班延误算是家常便饭的地方都不买保险的人,回来之后能买就买。说了这么多,我只是在小小思量明天应该怎么回家啊,这个高铁还敢不敢坐啊?查了查明天的高铁剩余车票,基本上京沪高铁都没怎么卖出去嘛!看来大家已经开始“用脚投票”了。
刚才在例行的看订阅的东西,就瞟见木遥终于更新了一篇学术日志:J-L 定理,以及为什么一个立方体相当于一个球壳。开始的时候没注意是他的,还在想谁能用中文写关于纯数学的blog;定睛一看之后,果然是木遥。这篇日志中提到的J-L定理,大致是:
Johnson–Lindenstrauss 定理是我在今晚的一个学术报告里听说的一个非常令人惊讶的定理。简单说来,它的结论是这样的:一个一百万维空间里的随便一万个点,一定可以几乎被装进一个几十维的子空间里!
本能的出于对中文写作的文献的不信任(无关作者国籍,只是说写作语言,中文论文噪音实在是太大了,甄别起来太费事儿),我顺手搜了搜,找到了一篇1999年的证明,上曰:
The Johnson-Lindenstrauss lemma shows that a set of n points in high dimensional Euclidean space can be mapped down into an O(log n=ffl 2 ) dimensional Euclidean space such that the distance between any two points changes by only a factor of (1 Sigma ffl).
到这里,基本和上面先引用的木遥深入浅出的解释一致了。Google scholar继续给力,一下子又看到了两篇应用这个定理的paper:
- Ella Bingham and Heikki Mannila. 2001. Random projection in dimensionality reduction: applications to image and text data. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining (KDD '01). ACM, New York, NY, USA, 245-250.
- Nir Ailon and Bernard Chazelle. 2006. Approximate nearest neighbors and the fast Johnson-Lindenstrauss transform. In Proceedings of the thirty-eighth annual ACM symposium on Theory of computing (STOC '06). ACM, New York, NY, USA, 557-563.
(还请大家暂时容忍我的引用不规范……不想开Zotero了)
第一篇文章便是应用了Random projections来进行降维处理,是一篇实证文章,比较了Random projections和其他经典方法的优劣,采用的是图像和文字数据;第二篇则是基于上面的J-L定理,发展出来的Fast-Johnson-Linden-strauss-Transform(FJLT)变换算法:The FJLT is faster than standard random projections and just as easy to implement. 看到这里,大致可以理解J-L定理的基本原理和相应的发展趋势了。当然,还有一些研究者在继续探究J-L定理的性质,比如这篇William B. Johnson , Assaf Naor, The Johnson-Lindenstrauss lemma almost characterizes Hilbert space, but not quite, Proceedings of the Nineteenth Annual ACM -SIAM Symposium on Discrete Algorithms, p.885-891, January 04-06, 2009, New York, New York。我就没有细细看此文了,以一个标题党的眼光这篇文章大致指出了J-L定理(或者引理?)还不足以完美的勾勒Hilbert空间的性质吧。
关注高维数据降维,一者是最近貌似高频大规模数据处理很热,姑且认为这种需求大概是近十几年计算机大规模应用在各个行业的必然结果吧;另者巧的是最近google不是出了个新的图片搜索么,可以直接拖图到搜索框中。正好看到了一篇blog论及与此,好奇之下也就在关注google的算法:
When you upload an image to Search by Image, the algorithms analyze the content of the image and break it down into smaller pieces called “features”. These features try to capture specific, distinct characteristics of the image - like textures, colors, and shapes. Features and their geometric configuration represent the computer’s understanding of what the image looks like.
- 对于每张图片,抽取其特征。这和文本搜索对于网页进行分词类似。
- 对于两张图片,其相关性定义为其特征的相似度。这和文本搜索里的文本相关性也是差不多的。
- 图片一样有image rank。文本搜索中的page rank依靠文本之间的超链接。图片之间并不存在这样的超链接,image rank主要依靠图片之间的相似性(两张图片相似,便认为它们之间存在超链接)。具有更多相似图片的图片,其image rank更高一些。
简而言之,Google不过是把图片的特征提取,从我的理解来看也是一种把高维数据进行降维处理的思路。
说来有趣,我本身不是一个学计算机出身的,虽然机缘巧合的在大学期间学了很多涉及编程的东西,但更多只是限于语法,还谈不上算法。总所周知,国内的算法和数据结构教材有够陈旧和不实用,所以当年算法就没学好……不过对于“时空复杂度”的基本概念还是有的。后来发现经济学里面居然也盛行编程,当然大多数是一种数值模拟的思路(计量除外)。只是这里大多情况下也用不到什么算法了,一个定理出来之后算法的思路基本就很明晰了,更多的只是在于如何更好地定义初始的数据结构,以及一些基本的小tricky的选择(比如是插值算法是牛顿插值还是其他)。另有一种感觉就是以现在计算机的高计算能力和大多数情况下经济学里面对于模拟的要求,根本不需要找个高效率的算法——大多情况下循环也循环不了多少次,计算机跑1秒和2秒的差别又何在?弄得我有时候就是偷懒,明知程序写出来很没效率,还是不愿把时间花费在思考一个更有效的算法上——只要找一台更好的计算机便是了嘛!于是在我的笔记本已然承载不了的情况下,开始折腾学校里面的计算机,哈哈。当然,已知的更好的收敛算法还是会考虑的,比如经典的"policy function iteration"和"value function iteration"……顿时想起当年严格证明前者的迭代结果和后者一样的痛苦经历……于是于我,心里便暗暗的有种感觉,算法不是学CS人的事儿,是学math的人的事儿……各种美妙的数学定理才是更好的算法的源泉啊。
另,木遥提到的另外的关于高维空间中大数定理的问题,也很有趣,值得稍稍琢磨一下。无奈我数学基础还不够,尚不能完全理解他说的那些东西,看来还是需要时日打磨啊。
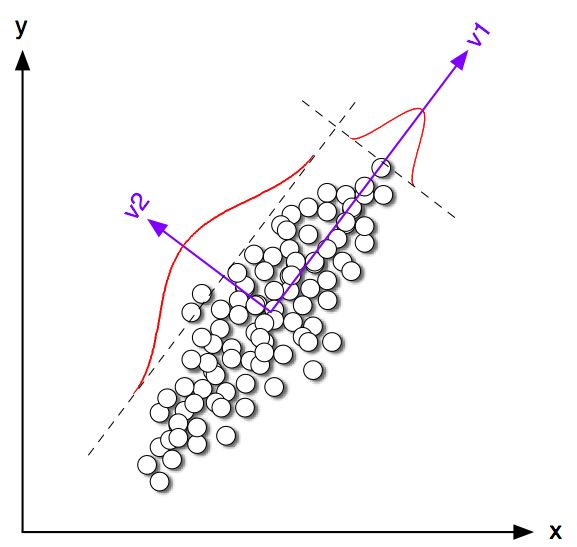
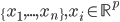 ,我们希望降到q维的
,我们希望降到q维的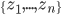 。从这个角度来讲,降维和聚类还是有相通之处的,都是对于特征的提取。只是一个从行的角度出发,一个对列操作的感觉。
。从这个角度来讲,降维和聚类还是有相通之处的,都是对于特征的提取。只是一个从行的角度出发,一个对列操作的感觉。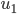 ,
,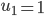 使得
使得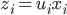 ,且
,且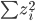 最大。
最大。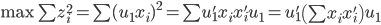 。所以我们只需要求一阶导数
。所以我们只需要求一阶导数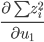 即可。
即可。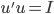 使得
使得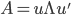 ,其中
,其中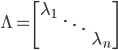 为A的特征值矩阵,故
为A的特征值矩阵,故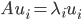 (列向量为特征向量)。不失一般性,我们可以排序使得
(列向量为特征向量)。不失一般性,我们可以排序使得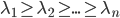 (从大到小排序)。
(从大到小排序)。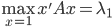
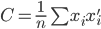 为x的相关矩阵,
为x的相关矩阵,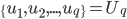 ,从而
,从而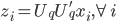
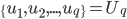 (q维的子空间)
(q维的子空间)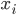 投影到该q维空间,这样
投影到该q维空间,这样 ,且
,且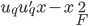 最小。
最小。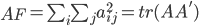
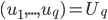 使得
使得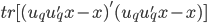 最小。
最小。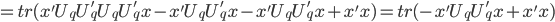 最小。
最小。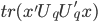 最大(注意没有负号)。
最大(注意没有负号)。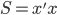 称为数据的相似矩阵
称为数据的相似矩阵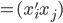 。
。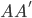 和
和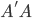 均为对称阵,且两个阵有相同的特征值。记
均为对称阵,且两个阵有相同的特征值。记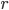 为A的秩,AA'的特征向量
为A的秩,AA'的特征向量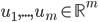 ,A'A的特征向量
,A'A的特征向量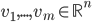 ,则
,则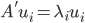 ,
,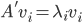 。做奇异值分解,则
。做奇异值分解,则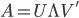 .
.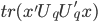 求得的和前述结果等价。
求得的和前述结果等价。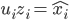 ,解
,解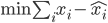 即可。
即可。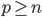 即数据非常高的时候,可以转置后再做。
即数据非常高的时候,可以转置后再做。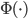 ,即实现非线性的降维。需要注意,降维的过程需要保持可逆。
,即实现非线性的降维。需要注意,降维的过程需要保持可逆。