聚类讲的比较简单...怎么感觉老师不怎么待见unsupervised learning捏?...
---------------笔记开始---------------------
1. 一般概念
1)分类与聚类(分类标识)
评测纯度。我们有测试集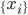 ,这样定义纯度为
,这样定义纯度为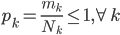 .
.
2) 输入
- 特征向量的表示:
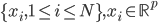 。
。 - 相似矩阵的表示:
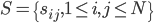 ,其中相似度的计算可以是
,其中相似度的计算可以是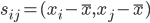 的内积。显然,向量表示很容易可以计算相似度表示。
的内积。显然,向量表示很容易可以计算相似度表示。 - 距离矩阵的表示(不相似度):
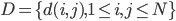 ,其中距离可以用二阶范数定义,比如
,其中距离可以用二阶范数定义,比如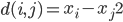 。
。
3) 输出: 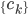 ,对应K个聚类。这里还分为:
,对应K个聚类。这里还分为:
- 非层次的
- 层次的(类似于树结构)
2. K-means方法(非层次聚类)
(注意不要和KNN搞混了,都是K开头的...)
1) K-means方法(特征表示)
输入: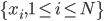 ,K——聚类的个数。
,K——聚类的个数。
算法:
初始化,随机选定类中心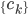 .
.
- (i)根据
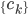 分配
分配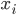 到距离最近的类。
到距离最近的类。 - (ii)修改
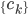 ,使得
,使得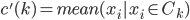 。重复上面两步。
。重复上面两步。
2) K-medoids方法(相似度表示)
输入:s,k
初始化。然后根据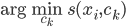 分配
分配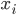 ,再按照
,再按照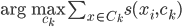 确定新的中心。
确定新的中心。
3) 模糊的K-means方法
输入: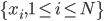 ,K
,K
初始化。
- (i)
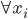 ,计算
,计算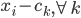 ,然后根据这个距离的比重来“软”分配
,然后根据这个距离的比重来“软”分配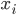 (需要归一化分配权重)。
(需要归一化分配权重)。 - (ii)
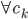 ,利用
,利用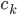 中的
中的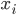 进行加权平均。
进行加权平均。
重复上述两步。
4) 谱聚类(向量表示)
输入: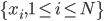 ,K
,K
然后对原始数据做转换,形成新的数据集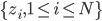 ,然后再做K-means聚类。
,然后再做K-means聚类。
其中转换的步骤如下:
- (i) 计算相似矩阵S
- (ii) 计算L=D-S,其中
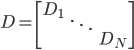 ,
,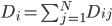 。
。 - (iii)计算L最小的K个特征值对应的特征向量
- (iv)让U=
 ,则
,则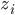 是U的第i行,这样就从p维降到了K维。
是U的第i行,这样就从p维降到了K维。 - (v)对Z进行K-means聚类。
3. 层次聚类
1) 自底向上的方法(聚合)
初始:每个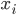 都为一类
都为一类
而后对于最相似的两类,合并到一类。对于类的最相似,可以定义为距离最近的类。而对于距离,则可以定义为三者之一:
- (i)
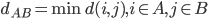 ,称之为单连。
,称之为单连。 - (ii)
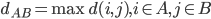 ,称之为全连。
,称之为全连。 - (iii)
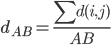 .
.
2) 自顶向下的方法(分裂)
初始:所有的x作为一类。选用一种非层次的方法进行聚类,递归使用。
例子:二分法。
初始: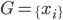 ,
,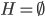 。而后选择离G最远的一个点g。
。而后选择离G最远的一个点g。
修改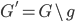 ,
,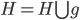 。重复步骤,选择离H近的离G远的逐渐加入H。
。重复步骤,选择离H近的离G远的逐渐加入H。
直到分不动了,彻底分为两类。
---------------------
下节课讲的是降维方法。