成天跟大数据打交道,最恨的就是out of memory这种错误。诚然,可以通过加大内存等方式来保证运行,但是随着数据量的增长,时间上的损耗也是很厉害的——比如时间复杂度为O(n^2)甚至更高。所以为了一劳永逸的保证计算的运行,需要在算法的改良上做一些文章。有了一个简单的类似于binning的idea,就去厚颜无耻的骚扰施老师了。
然后就顺利的套到了一篇paper,我能说我是瞎猫走狗屎运了么?居然还真问对人了,如获至宝的搞到一篇paper:
Yu, Bin, and Tao Shi. "Binning in Gaussian Kernel Regularization." (2005).
兴致勃勃的读起来,page 1 the history, interesting; page 2, ok...loss and penalty function ; page 3, oh...; page 4, fine...page 5, what the hell?瞬间扑面而来的各种公式一下子把我打回了原形——没学过就是没学过,再装还是读起来一片茫然。
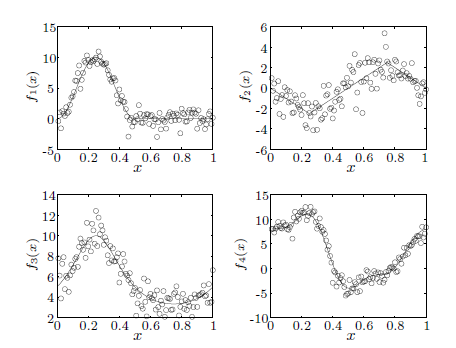
然后开始迅速的往后找,找到了binning method的定义,嗯,不就是画格子嘛,和我本来要的思路差不多,多少找回一点感觉(binning的想法就是直方图,只不过是高维的扩展,把点aggregate到一个个格子,然后统计频数就可以啦,或者固定点的数量来确定格子)。跳过若干公式...直到后面的结果,眼前一亮:
嘻嘻,就是这个!时间缩短至0.4%!神啊,比我想象的效率还高很多。这点loss in accuracy完全可以忍受嘛,重要的是——时间!时间!
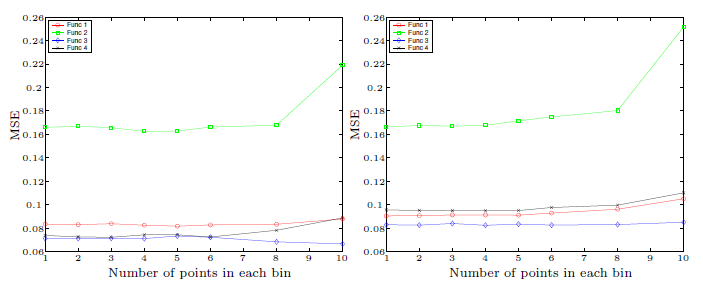
然后问题就是,这个binning该怎么定义为好呢?看他simulate的结果,嗯,好像在这个case中每个格子的点到了9以上误差开始上升。
还好啦对不对。具体的格子数量可以用实际数据测试一下,看看哪个更符合实际需求,直觉上应该是跟X以及Y的(联合)分布有关的...
好吧,我这是高射炮打蚊子么?我只是想在一个很简单的线性回归上面做一些binning...喵。多学一点总是好的,俗语嘛,“不畏浮云遮望眼,只缘身在最高层”。
p.s. 我也不知道为什么作为一个算法基础极为薄弱的、数学公式看起来依然会晕晕的、看到各种hilbert space开始感觉眼前飘过一团云雾的孩子会开始研究算法的问题...真的是被折磨太久了么?不过有时候看看这类的paper还蛮有裨益的...