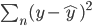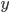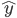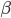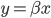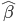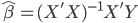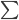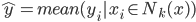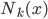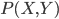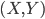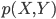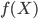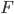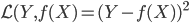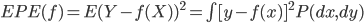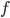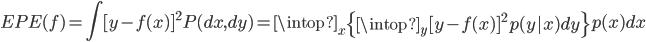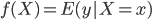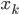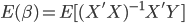Tag: k-means

从Variance说起：回归、聚类、残差和方差

前言的废话：有种被统计学洗脑的感觉，跟搞统计的接触的有点太多了吧...哎，算了，难得有点感悟记录一下吧...喵。本文试图以一个典型的统计学的思维过程来叙述，呃，可能功力不足，凑合着看吧，也不枉我连续几天做梦都是直方图密度曲线 average treatment effect之类的。

-------------------------------------------废话结束了-----------------------------------

Variance这个词很好玩，如果是用在统计的情境中就中文译作方差，公式就是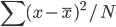，写成列向量（N*1矩阵）的形式就是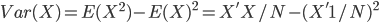，1这里是N×1个1的列向量。从公式的形式就可以看出是一个二阶中心距，即距离中心的距离的平方（二阶）和。然后既然是二阶距，那么自然的衡量的就是某个数据集分布的离散情况。越大越散，越小越密。此为一维（这里指只有一个观测维度的情形）相信这样的定义实在是太耳熟能详了。方差有个小弟叫做标准差，就是方差开平方。这个也没啥说的，有意思的是大家习惯用字母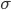来标注他，于是有了著名的六-西格玛原理...好吧，其实最有用的就是正态分布的几个西格玛了（随便偷张图）：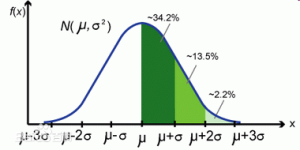

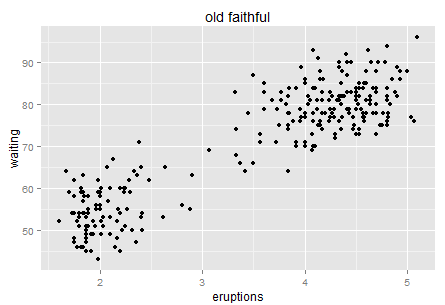
然后我们看简单的二维。二维就是散点图，没什么特别说的。找张著名的散点图来（~~随便找的，懒得自己去R里面画了~~。最后还是乖乖的去R里面的画了，还是自己画的好用一些，果然偷懒不容易，唉，我写博客实在是太敬业了！）。

背景知识大家可以去自己搜搜，反正就是黄石公园某个自然形成的间歇性喷泉，每次喷发的时间和等待时间的散点图。挺简单的对吧。这个数据点也不多，大家一眼扫过去大概百余个的样子。可是这幅图真的很有意思，跟Variance的联系实在是太紧密了。

我们先来说直觉。如果让你用自然语言（而非统计或者数学公式）来讲述这个图，比如你带这你刚上小学的孩子去黄石公园玩，他好奇的在等待这个喷泉喷发，这个时候你应该怎么跟他讲？嗯，可以大概说一下，“你看基本上呢，你等的时间越久，下一次喷发的时间就越长哦。让我们一起来计时~” 然后小朋友看了一眼图，不服的说到，“什么嘛，明明是等了如果超过一小时（或70分钟），那么下一次基本上喷发时间才会长(4-5分钟）。”。那么到底哪种说法更准确呢？

（吐槽君：自从上次写了乐高机器人之后，落园的段子里面的科普对象就从同学们降低到小朋友了，喵~）

好啦，不跟小朋友玩了，我们得研究一下更fancy一点的方法。说白了就是，用一个什么样的模型可以让经过我们模型处理的Variance尽量的小呢？

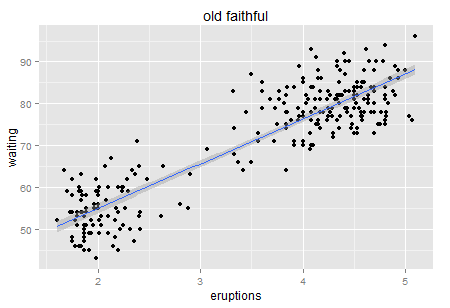
嗯，同学们说试试回归呗，明显的正相关性啊。你都说了啊，X的增加Y也在增加（先不要理会因果即X和Y谁先谁后，我们只说相关）。

所以我们虽然得到了一个显著的正相关关系，但是回归模型的R方只有81%（当然已经很好了，只是我们希望更好嘛）。来看看对应的残差分布：

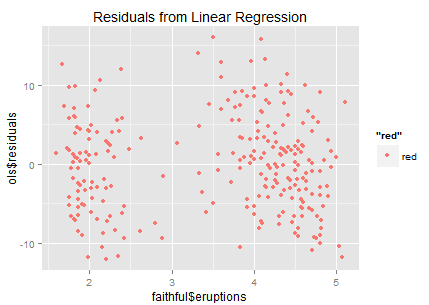残差好像挺散的（最理想的残差就是白噪音了，说明没有任何信息量了），但是隐隐约约也能看出来有两群这样。于是很自然的，有同学说，我们去试试聚类啊。

在去试聚类以前，先说说大名鼎鼎的K-mean算法的一些基石。

上面不是罗嗦了一堆variance在一维情形下的定义嘛，那么推广到二维，也很简单。

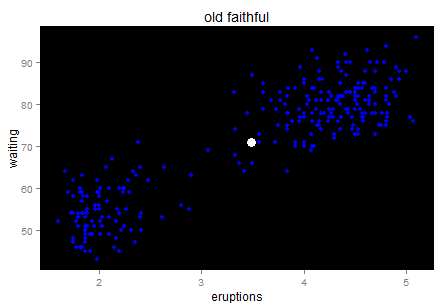
定义二维的中心点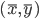：，然后就可以定义二维方差：每个点到图中心的距离的平方和。看图就知道了。

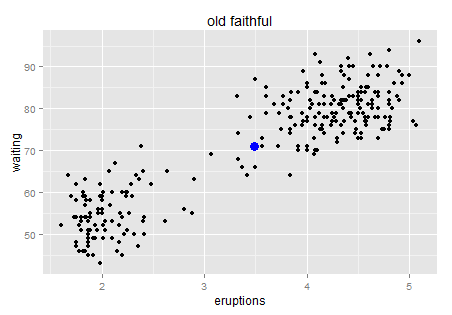蓝色的就是中心点。这里我们就不罗嗦什么均值容易受极值影响之类的了，那些也是看菜下料的，我们的数据看起来还好。（突然间为什么有种牛郎织女鹊桥相会的即视感...原来古人观星也是有异曲同工之妙呀，天空就是一个大大的散点图——勿喷，我保证下面不跑题了）

对于一个线性回归模型来讲，我们看的就是残差项的方差——残差项方差越大，表示他们分布的越散，那模型捕捉到的信息就少。

对于聚类呢，也可以看相应的方差：每个类里面的点到类中心的距离平方和 -> K-means。K-means虽然是通过迭代来实现的，但他的原理大致也是让二维的二阶中心距最小（由每一次迭代的损失函数来决定）。一眼扫过去大概可以分成牛郎织女两堆星星，那么我们就聚两类好了。显然不用跑程序我们也知道，聚成两类之后的组内方差和肯定比直接跟中心点算一个方差要小。

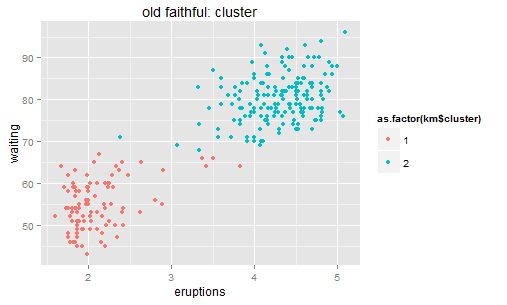聚成两类之后呢，我们类似定义的残差就是两类中每个点距离其中心点的Y轴距离（因为会直接把中心点作为每类的预测值）。还是画个残差图看看。

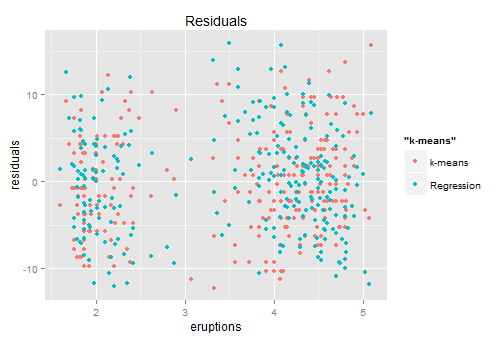红色是K-MEANS给出的残差，蓝色是回归给出的残差。貌似这两个长得还是挺像的，也是左右两群，虽然每群中两者长得都不太一样...这个时候我们就可以回到和小朋友的对话了：你们说的都有道理，都有8成的准确率，谁也没比谁更好很多。

于是我们尝试在每组内再做回归？会有效果么？

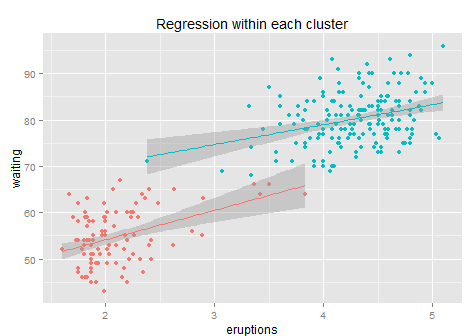见效寥寥...引入聚类后回归模型的R方从81%升到了84%，才3个百分点。这主要是在每一类里面，我们很难找到残差的规律了，所以这样只是通过组别信息的增加减少了组间方差，而其实从上图我们也可以看出每个组内的残差方差还是很大的、每条回归拟合线的斜率从最初的10降低到6和4，每个子回归的R方只有10%不到，能给予的信息已经很少了，所以整体模型只是增加了一点点准确性。但是无论如何也比直接玩回归的效果要好（之所以用k-means而不是简单粗暴的用类似x>3.5这样来分成两类，是因为k-means是按照其损失函数优化过的、给出的是最优的两类聚类结果）。

问题来了，为什么我只聚成两类而不是三类五类甚至更多呢？主要是怕过拟合，数据才200多个点，聚太多的话很容易过拟合了。大数据的情况下可以尝试其他办法。

好了，废话了这么多，其实统计学家们已经不仅仅玩这些了。其实我们上面的残差图传达了一个很重要的信息就是残差的分布不是一个白噪声（或者说不是均值为0、方差为常数的正态分布），称之为异方差(Heteroscedasticity)。异方差有很多很多情形，最简单的就是随着X的增加而增加。还是网上随便找了个图：

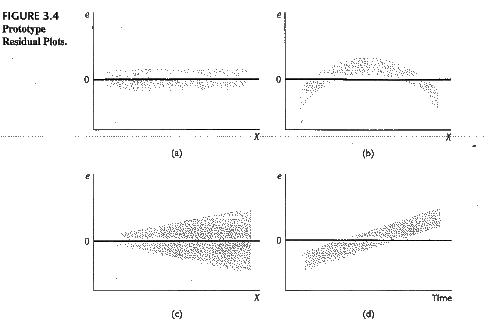异方差的存在使得我们模型的估计（或者基于训练数据预测）精度有限（先不考虑validate- test那些），所以统计建模常年在跟残差项的分布作斗争——反正看到你有什么规律，我就可以提取出来更多的信息放到我的模型中。计量经济学家喜欢说残差项是垃圾桶，但其实也是金矿——没办法呀，资源有限，不能太浪费。

然后是一些补充的废话时间。

Tags Eicker–Huber–White, k-means, variance, 三明治矩阵, 分位数回归, 回归模型, 实验分析, 异方差, 方差, 残差, 社会实验, 稳健标准误, 聚类, 贝叶斯, 频率派, 黄石公园

读书有感

社会网络中的社群识别（Community Discovery）概述

Post author By Liyun
Post date November 24, 2013
20 Comments on 社会网络中的社群识别（Community Discovery）概述

最近一直在看Community Discovery这一块儿的论文，深深的感觉现在就是一个矿工，不断的想方设法挖出来更有价值的信息。而且不是一个点一个点的突破，而是需要寻找出一种脉络，串联起所有的信息来。头痛。

最近的情况是，有一个well-connected的网络，然后我想把它稀疏化、打散成一个个独立的community的感觉。这样就可以分别识别每个community的特征什么的。所以厚着脸皮找施老师讨了几篇papers。而主要的问题是，数据太大了...11M nodes， 20 M edges，还是directed weighted network...我直接放弃了把这些数据从SQL Based data source中挪出来的想法，还是先努力的减少一些edges吧。

先罗列几个相关的术语：community discovery, graph partitioning, network clustering, network sparsification, modularity。了解一个领域最好的方法大概就是去读literature review了，所以乖乖的要了一篇:

Srinivasan Parthasarathy, Yiye Ruan and Venu Satuluri. "Community Discovery in Social Networks: Applications, Methods and Emerging Trends", in Social Network Data Analytics 2011. (NS, DM)

最契合我的想法的就是cut类方法——remove some edges to disconnect the network, then （drop isolated nodes with degree = 1 (could be added back later as auxiliaries to each community)。

那么就先从这一类方法开始说。比较经典的算法呢，是希望砍掉一条边以后，community内部的凝聚力不变，外部连接变差。基本上常用的就是Ncut（normalized）和Conductance、KL object、Modularity这些指标。比如KL算法，就是从二分图开始，不断迭代的去寻找如果交换某两个点所属community就可以减少edge cut的边。可惜的是，这些最优化问题都是NP-hard....随着数据的增大算起来会异常吃力。KL算法本身迭代也是相当考验计算能力的（贪心搜寻）。

然后就是凝聚（或者切分）类算法。凝聚就是先各自为家，然后附近的相互结合在一起，直到理想数量的社群结成；切分则是先从一个整体开始，然后每一步都切成两份这样。这些都算是层次聚类，最后可以给出一个长得像二分树的系统树图。这一类算法有Girvan和Newman切分法：每一步先计算每条边的betweeness score，然后把得分最高的边砍掉，然后再重复这个步骤。嗯，问题依旧是这样的迭代很耗时间。

频谱类算法（spectral algorithms)。听这个名字一股经典风就袭面而来。基本上这类方法就是仰仗特征向量（eigenvector)，比如adjacency matrix的特征向量，然后top k特征向量就定义出来一个k维的特征空间，然后就可以用传统的比如k-means这样的方法来聚类了。说白了就是降维、降维。可惜这种方法依然算起来很消耗资源，光算那个特征向量就是O(kM(m))的复杂度...基本在大矩阵下就投降了。一个概率的方法就是Graclus算法，基本的直觉就是基于加权的normal cut measures再做加权核k-means便可以给出基于特征向量聚类一样的结果，而计算消耗相对少一些。

多层次图分割(Multi-level graph partitioning)。这个就是相比而言快速有效的方法了。基本的想法就是，先压缩原始图像到一个小的图像、分割这个图，然后再映射回原来的图。毕竟小图分割起来就要快的多嘛。这类的方法除了上面说到的Graclus，还有Metis（以KL object作为measurement），以及MLR-MCL。

马尔可夫聚类（Markov Clustering，MCL）。基本的想法就是，两点之间的信息传递是随机流（stochastic flow）。MCL对随机矩阵会做两个操作，扩张（expand）和膨胀（inflate）。前者就是简单的矩阵平方，后者则是用一个膨胀参数（非线性）来撑大彼此之间的差距，最后再重新normalize。这两个步骤交替进行。这样的话，原本community中紧密相连=的两个点则会更紧密的相连，而不同cluster之间的连接则被弱化。这样最后每个community之内的点都会流向某个attractor（吸引点），从而我们可以识别各个cluster。感觉这里有点收敛到一些不动点的意思。MCL的弱点也是计算消耗。矩阵乘法在开始边的权重没有弱化的时候是非常消耗时间的，此外MCL倾向于产生不平衡的群落，尤其是可能产生一堆很小的群落或者一个很大的群落。

MCL的改良主要是在引入惩罚项（regularized MCL）和加入多层次（multi-level regularized MCL），以减少不平衡的clusters和解决MCL难以scalable的问题。后者也简称为MLR-MCL，就是刚才多层次分割里面有提到的那个。

局部聚类(local graph clustering)。局部方法基本上就是从一个给定的顶点(seed)出发，寻找符合条件的群落，而并不关心整个graph的情形（除非所有的群落需要覆盖全图）。计算上就是利用随机游走（random walk），从一个群落的内部开始，一点点的向外扩张（有没有很像page rank的感觉？）。最早的Spielman and Teng就是这样的基于顶点随机游走的算法。后面Andersen and Lang改进了这类方法，可以从一堆seed sets出发而不是单单一个顶点。此外，Andersen还试图在随机游走之上加入re-start(即个性化的pagerank)。

再需要提及的就是在动态网络(dynamic network)之上的community discovery——不同于静态网络，动态网络是本身一直在变化的，正如我们一直在用的facebook、twitter这般。还有异质网络（heterogeneous network）和有向网络(directed network)。呃，这部分我就没细看了，貌似蛮复杂的样子...就是其中有一个Community-User-Topic（CUT）model看起来蛮有意思的，准备明天去找这篇paper读一下：

D. Zhou, E. Manavoglu, J. Li, C.L. Giles, and H. Zha. Probabilistic models for discovering e-communities. In WWW ’06: Proceedings of the 15th international conference onWorldWideWeb, page 182. ACM, 2006.

嗯，到总结了~前面一直在说的就是计算、计算、计算。

可扩展的算法（scalable algorithms）：这里主要是牵扯到分布式计算。multi-level类的算法是有分布式的潜力的，然后GPU和多核计算貌似也能对流算法(streaming algorithms)帮上忙。
群落和其进化的可视化：可视化主要是可以帮我们更直观的理解动态网络的变化、提供分析的直觉、以及帮助验证分析结果。
结合业务知识：这个也不仅仅是对这些群落识别算法啦，任何一个机器学习的算法都离不开基本的业务知识吧。
排序和加总：基本上还是缺乏对于得到的群落之间的排序（打分）、加总的研究。

好了，到此为止~继续看其他paper去了。

读书有感

≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记（二）

Post author By Liyun
Post date October 19, 2012
5 Comments on ≪统计学习精要(The Elements of Statistical Learning)≫课堂笔记（二）

继续一周一次的课堂笔记昨天去晚了站着听讲，感觉好好啊，注意各种集中。想想整个教室里面就是我和老师是站着的，自豪感油然而生。

第二次课讲的东西依旧比较简单，是这本书第二章的前半部分。作为一个好久之前已经预习过的孩子，我表示万分的得意（最小二乘法难道不是三四年前就学过的？话说以后我再面人的时候，就让他推导最小二乘估计量，嘻嘻...考验一下基本功）。

------------原谅我的废话，笔记开始------------

简单预测方法：最小二乘法（以下沿用计量经济学的习惯，简称OLS）

OLS实在是太普遍了，我就不赘述细节了。OLS的思想就是，基于已有的样本信息，找出一条直线，让预测值与真实值之间的残差平方和最小，即最小。其中，为真实的样本观测值（已有样本），而是OLS的预测值。用图来讲的话，X为一维向量的时候，就是用一条直线来最好的拟合各个样本点。

这里就很明显了，首先OLS假设是一条直线。那么就是一个参数模型，即我们需要假设一个未知的参数，构成一个线性方程，然后再去估计的值。然后呢，直线会有很多条，所以我们要找到一个目标——比如这里，就是最小化残差平方和RSS。换言之，我们寻找的就是最优的向量使得RSS最小。

解这个最优化问题很简单，我就不重复了。最后解得的最优估计量为：

这里写成矩阵形式，比较简单。X为一维向量的时候，可以改写成形式，我个人不大喜欢，就不展开了。

简单预测方法：K近邻（k nearest neighbor）

K近邻的思想就更简单了。不就是想预测某个点x对应的y么？那么就把它的邻居都找来，平均一下好了。不是有句话叫做什么“一个人的收入就大概是他的圈子收入的平均值么？”

所以，这里表示点x的K近邻。至于这个近邻怎么定义嘛，嘻嘻，很简单啊，欧几里德距离就可以嘛~

评语：吴老师对于这两个算法的直观评价是，OLS呢就是勤奋的学生，预测前先做足功课，预测的时候只要知道X，噼里啪啦一下子y就估计出来了。然而knn则是一个临时抱佛脚的学生，预测的时候开始找自己的k近邻，然后把它们平均一下就好了。哈哈，大意如此，大家可以体会一下这种精神。我个人感觉呢，OLS属于以不变应万变的，而knn则是见机行事的。

统计决策理论(Statistical Decision Theory)

说了这么多，这个模型好不好到底怎么判读呢？凡事总得有个标准呢。这一系列的标准或者说准则，就是统计决策理论了。

首先呢，大致我们需要对X,Y有个分布上的描述：用记作向量的联合分布，然后为其对应的密度函数。之后为了估计Y，我们会有很多很多模型，即各种，而这些组成的函数空间记为。

然后我们定义一个损失函数，比如在均方误差意义下，，这样就有了一个选择的标准——使得损失函数的期望最小：。接下来就是，到底在空间里面，哪一个最符合这个标准呢？

首先自然是把联合分布变为条件分布。这个idea显而易见——我们总是知道X的（原谅我吧，全中文确实比较难写，偶尔穿插英文一下 ^_^）。所以conditional on X，我们就有了

去解最小化问题，最终我们得到的就是在每个点X上，。通俗的讲就是，对于每个点预测，把和它X向量取值一样的样本点都找出来，然后取他们的平均值就可以了。很直观的不是么？这里也有点最大似然的想法呢——比如预测一个男孩的身高，最保险的就是把和它同龄的其他男孩的身高平均一下，不是么？

但是说来简单啊，很多时候都是未知的，根本无法计算嘛。所以只能近似：

回忆一下knn，就是放松了两点：1) 取的是x的近邻，而不一定是x； 2)用样本平均数代替了期望
而OLS呢，也是最后在这里，用样本平均代替了期望。

近似嘛，自然有好的近似和不好的近似。很显然的，当样本比较大、尤其是比较密集的时候，x的邻居应该都离x很近，所以这个误差可以减小；此外，当样本很大的时候，根据大数定律，平均数收敛于期望。所以，这两种算法应该说，都在大样本下会有更好的效果。

模型选择、训练误差与测试误差、过拟合

这里讲的比较简单。模型选择就是的选择，即选择哪一类函数空间，然后再其中找/估计最优的。很显然，如果只有若干个有限的样本，我们总能把各个样本用直线或者曲线依次连起来，这样的话就有无数个f可以作为此问题的解。显然这不是我们想要的——这样的称为“不设定问题”，即可能无解、可能多个解、还可能因为一点点X的变化导致整个解的解答变化。因此我们需要先设定一个解的类别。

训练误差：预测模型估计值与训练数据集之间的误差。RSS就是一个典型的训练误差组成的残差平方和。

测试误差：用训练集以外的测试数据集带来的误差，显然我们更关心的是测试误差——训练总能训练的很好，让损失函数期望最小，然而测试集则不一定这样。一般说来，测试误差>训练误差。

过拟合：选择一个很复杂的f，使得训练误差很小，而实际的测试误差不一定小。最极端的就是刚才说的，把训练集的点一个个依次连起来...训练误差肯定是0是不是？

我们关心的自然是怎么降低测试误差。显然这东西会跟训练误差有关，但是它还跟f的复杂度有关。最最棘手的就是，f的复杂度是一个难以衡量的问题。早期的研究有用自由度来衡量这个复杂度的，但是也不是那么的靠谱...后面的有人鼓捣出来PAC(使得近似正确的概率最大——吴老师原话)，还有一个VC来衡量复杂度——但几乎实践中无法计算，没几个计算出来的。嗯，水很深哇。

Tags k-means, K近邻, OLS, 吴立德, 回归, 复旦, 数据挖掘, 最小二乘法, 有监督学习, 机器学习, 模型选择, 测试误差, 统计学习精要, 训练误差, 读书有感, 过拟合