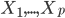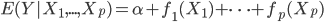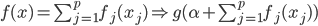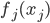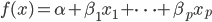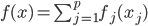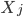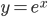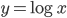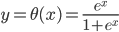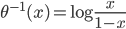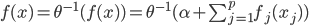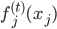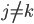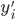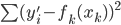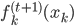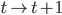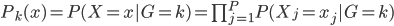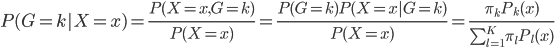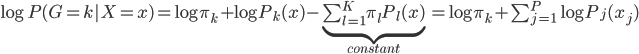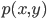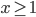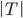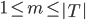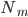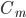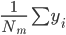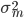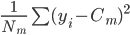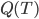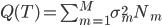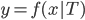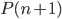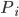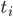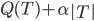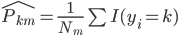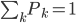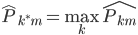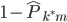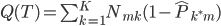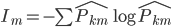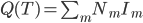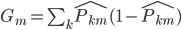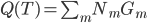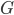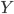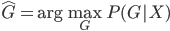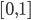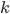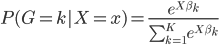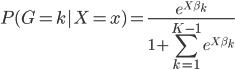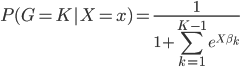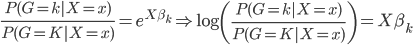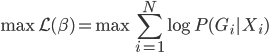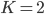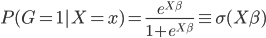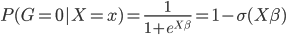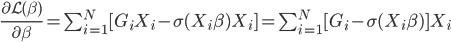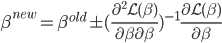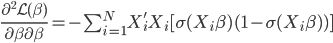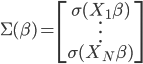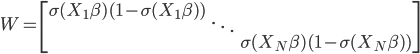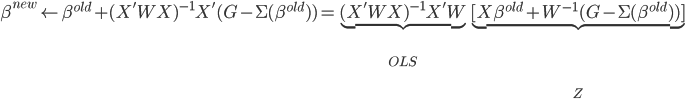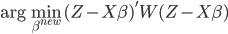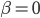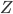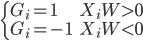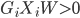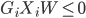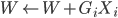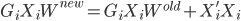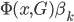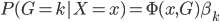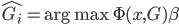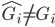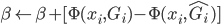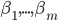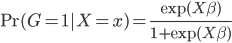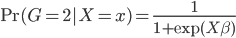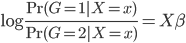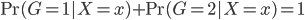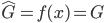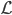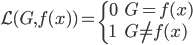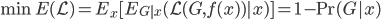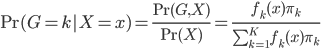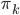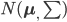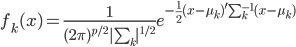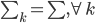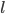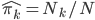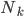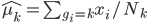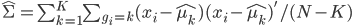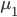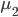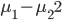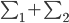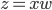第九章 可加模型、树模型相关方法
1. 可加模型(additive model)
大家都知道线性模型是最简单好用的,但是往往现实中很多效应都是非线性的。前面举过一个学历的例子,再抄一下:
一方面,学历是你受教育的体现,也就是在取得学历的过程中完成了一定程度的知识积累。当然一定程度的学校录取证实了你一定程度的才智,但是也不是只有天才没有汗水就可以毕业的。更有意思的是,知识的积累往往是厚积而薄发,或者说是个非线性的...这也是为什么在衡量劳动者劳动价值的时候会放入受教育年限和其二次方的一个缘故(至少我是这么理解那个著名的xx公式中的二次方项的)。
也就是说,在线性模型中,我们最简单的方法就是利用多项式拟合非线性,不是有个著名的魏尔斯特拉斯(Weierstrass)逼近定理么?闭区间上的连续函数可用多项式级数一致逼近。
这个定理貌似在数分、实变、复变、泛函都有证明(如果我没记错名字的话)...泰勒(局部展开)也是一种局部使用多项式逼近的思路。不过 人类的智慧显然是无穷的,自然有了应对各种各样情况的“万能药”和“特效药”,任君对症下药什么的。
这一节主要是讲generalized additive models,即广义可加模型。广义可加模型假设的是:各个自变量之间不相关,即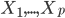 可以被拆分开(虽然书上是用期望定义为
可以被拆分开(虽然书上是用期望定义为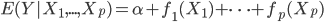 ,但是我觉得加入一些人为认定的交叉项再扩展开是没有问题的~)。数学表达式就是:
,但是我觉得加入一些人为认定的交叉项再扩展开是没有问题的~)。数学表达式就是:
(1) 定义: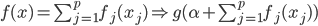 ,其中
,其中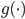 是已知的,而
是已知的,而 和
和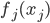 是需要估计的。可见,如果只是从我们线性模型的
是需要估计的。可见,如果只是从我们线性模型的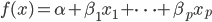 进化到
进化到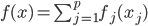 ,那么我们是放松了对于
,那么我们是放松了对于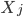 是线性的要求,可以对每个自变量进行非线性回归,但y和这些
是线性的要求,可以对每个自变量进行非线性回归,但y和这些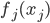 之间依旧是线性关系;如果进一步放松,那么就可以引入新的非线性函数
之间依旧是线性关系;如果进一步放松,那么就可以引入新的非线性函数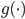 ,那么y和那一堆
,那么y和那一堆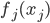 之外还可以再套一层非线性函数。不过这里就要求给定一个g了,常用的就是那些指数函数对数函数等。
之外还可以再套一层非线性函数。不过这里就要求给定一个g了,常用的就是那些指数函数对数函数等。
不过这里我们还要要求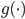 有一些比较优良的性质,首当其中就是可逆...(对于连续函数来说,可逆必定单调...因为可逆
有一些比较优良的性质,首当其中就是可逆...(对于连续函数来说,可逆必定单调...因为可逆 一一映射,又是连续的函数,不单调这就没法玩了呀!)好在我们一般就用一些比较简单的exp和log...常用的
一一映射,又是连续的函数,不单调这就没法玩了呀!)好在我们一般就用一些比较简单的exp和log...常用的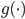 有:
有: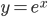 ,
,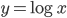 ,
,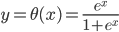 ,这样
,这样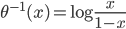 ...其中最后一个就是我们常用的logit regression。这样我们就可以定义“广义可加的logit模型”:
...其中最后一个就是我们常用的logit regression。这样我们就可以定义“广义可加的logit模型”: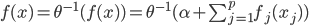 。
。
(2) 算法。还是一样的,有了大致的idea我们还得有好用的算法。下面介绍一种比较一般性的方法。
数据集依旧记作: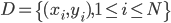 ,然后我们使用OLS准则:
,然后我们使用OLS准则: 。然后我们有迭代算法:即已知
。然后我们有迭代算法:即已知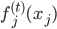 ,如何迭代到t+1?
,如何迭代到t+1?
p个小步:每一次我们都是用给定的其他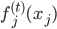 ,其中
,其中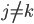 ,求得
,求得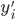 ,来最小化计算第k个变量的系数
,来最小化计算第k个变量的系数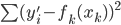 ,求的
,求的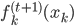 。这样的方法称为一维平滑值(one dimension smoother)。而在这个过程中,需要利用B-splines来求
。这样的方法称为一维平滑值(one dimension smoother)。而在这个过程中,需要利用B-splines来求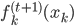 。所以“其实本来该模型的卖点是非参数,但是最后做一维平滑的时候还要利用参数化的B-splines...”,所以有点打折扣的感觉对不?
。所以“其实本来该模型的卖点是非参数,但是最后做一维平滑的时候还要利用参数化的B-splines...”,所以有点打折扣的感觉对不?
每p个小步构成一个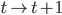 的大步。如果最后是用B-splines来拟合,那么其实一开始就可以代入各种参数一次性完成参数化计算。
的大步。如果最后是用B-splines来拟合,那么其实一开始就可以代入各种参数一次性完成参数化计算。
唯一值得考量的就是,这个迭代可能是局部最优化而不是全局最优化,有点取决于起始值的味道...我有点怀疑这个起始函数要怎么给...
(3) Na?ve Bayes Assumption(朴素贝叶斯假定)
有个有趣的结论:在Na?ve Bayes 假定下,分类器一定是可加模型。
直觉上讲,Na?ve Bayes假定其实也是假定分量独立: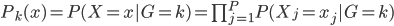 。
。
这样就很容易推导这个结论了:我们有后验概率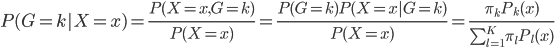 。取个对数,我们有
。取个对数,我们有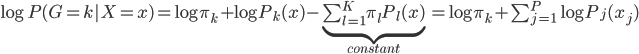 ,所以就成了可加模型的形式。这样,Na?ve Bayes 假定比可加模型的假定就更弱一点。关于这点,我又去搜了一下,呃,找到了一点有关的信息,抄如下:
,所以就成了可加模型的形式。这样,Na?ve Bayes 假定比可加模型的假定就更弱一点。关于这点,我又去搜了一下,呃,找到了一点有关的信息,抄如下:
- In supervised classification, inputs x and their labels y arise from an unknown joint probability p(x; y). If we can approximate p(x,y) using a parametric family of models G = {pθ(x,y),θ in Θ}, then a natural classifier is obtained by first estimating the class-conditional densities, then classifying each new data point to the class with highest posterior probability. This approach is called generative classification.
- However, if the overall goal is to find the classification rule with the smallest error rate, this depends only on the conditional density p(y|x). Discriminative methods directly model the conditional distribution, without assuming anything about the input distribution p(x). Well known generative-discriminative pairs include Linear Discriminant Analysis (LDA) vs. Linear logistic regression and naive Bayes vs. Generalized Additive Models (GAM). Many authors have already studied these models e.g. [5,6]. Under the assumption that the underlying distributions are Gaussian with equal covariances, it is known that LDA requires less data than its discriminative counterpart, linear logistic regression [3]. More generally, it is known that generative classifiers have a smaller variance than.
- Conversely, the generative approach converges to the best model for the joint distribution p(x,y) but the resulting conditional density is usually a biased classifier unless its pθ(x) part is an accurate model for p(x). In real world problems the assumed generative model is rarely exact, and asymptotically, a discriminative classifier should typically be preferred [9, 5]. The key argument is that the discriminative estimator converges to the conditional density that minimizes the negative log-likelihood classification loss against the true density p(x, y) [2]. For finite sample sizes, there is a bias-variance tradeoff and it is less obvious how to choose between generative and discriminative classifiers.
简单的说,就是“判别式模型与生成式模型”的问题。如果我们使用参数方法逼近联合分布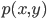 ,那么就是生成式模型(generative models);相对的,如果我们直接对条件密度p(y|x)建模而不对p(x)进行任何假定,那么就是判别式模型(Discriminative methods)。我们常见的就是LDA和线性logit模型、朴素贝叶斯和广义可加模型。在一些已知如高斯分布的情况下,我们发现LDA优于logit并且有更小的方差,但是生成式模型的问题就是他的参数假定不满足...所以估计可能是有偏的。所以现实中,我们需要在无偏性和方差之间做一个trade off。关于这里的总结我搜到一篇:Discriminative vs Informative Learning - Stanford University,习惯中文的可以参考一下这个。其实这里看看这些概念和思想之争也挺好玩的,以前完全没有从这个角度看过回归模型...可见计量经济学关心的完全不是这些东西。我现在完全没概念我在machine learning这个深潭里面到底涉足多深了,但是可以明显的感觉统计学习的一些思维已经开始影响我的思维方式了...需要再继续融会贯通一下。
,那么就是生成式模型(generative models);相对的,如果我们直接对条件密度p(y|x)建模而不对p(x)进行任何假定,那么就是判别式模型(Discriminative methods)。我们常见的就是LDA和线性logit模型、朴素贝叶斯和广义可加模型。在一些已知如高斯分布的情况下,我们发现LDA优于logit并且有更小的方差,但是生成式模型的问题就是他的参数假定不满足...所以估计可能是有偏的。所以现实中,我们需要在无偏性和方差之间做一个trade off。关于这里的总结我搜到一篇:Discriminative vs Informative Learning - Stanford University,习惯中文的可以参考一下这个。其实这里看看这些概念和思想之争也挺好玩的,以前完全没有从这个角度看过回归模型...可见计量经济学关心的完全不是这些东西。我现在完全没概念我在machine learning这个深潭里面到底涉足多深了,但是可以明显的感觉统计学习的一些思维已经开始影响我的思维方式了...需要再继续融会贯通一下。
2. 树模型(Tree Model)
(1) 树的一般概念:见过二叉树么?差不多的样子可以有多个叉叉...自行脑补一下分形去吧。
(2) 回归树(regression tree)
还是数据集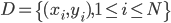 ,然后我们可以根据不同的门限来分类,比如x<;1分在左边枝子上
,然后我们可以根据不同的门限来分类,比如x<;1分在左边枝子上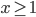 放在右边枝子上。然后在下一层继续分叉分叉...一层又一层。感觉当初发明树模型的孩子一定很喜欢生物学尤其是植物学吧!有没有类似于顶端优势的定理呢?嘻嘻,可以叫做歪脖子树定理嘛!
放在右边枝子上。然后在下一层继续分叉分叉...一层又一层。感觉当初发明树模型的孩子一定很喜欢生物学尤其是植物学吧!有没有类似于顶端优势的定理呢?嘻嘻,可以叫做歪脖子树定理嘛!
 (八卦来源)
(八卦来源)
对于一颗树T,我们采用如下记号:
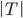 :叶子的总数
:叶子的总数
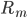 :
: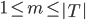 ,某个叶子或者根节点。
,某个叶子或者根节点。
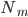 :叶子节点
:叶子节点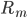 中的样本数。
中的样本数。
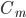 :
: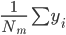 ,这
,这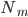 个点y的平均值。
个点y的平均值。
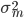 :
: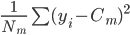 ,每个
,每个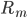
中的均方误差(方差)。
这样一颗树的质量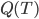 就可以定义为
就可以定义为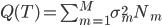 。这样给定一棵树,有了一个函数
。这样给定一棵树,有了一个函数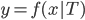 ,然后就可以预测了。
,然后就可以预测了。
树的生长:这就是叶子和层次的选择,显然我们一共有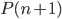 中选择。需要从中选出最好的
中选择。需要从中选出最好的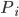 和
和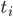 。当生长不动的时候,停止。而长得太大的时候,就是过拟合的问题。所以我们需要剪枝。
。当生长不动的时候,停止。而长得太大的时候,就是过拟合的问题。所以我们需要剪枝。
树的剪枝:准则需要变,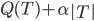 ,即加入一个惩罚项,然后就可以使用cross-validation或者bootstrap了。
,即加入一个惩罚项,然后就可以使用cross-validation或者bootstrap了。
(3) 分类树
同样的,只是我们需要定义新的准则,类似于0-1准则。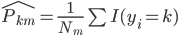 ,也就是节点中属于第k类的比例,所以
,也就是节点中属于第k类的比例,所以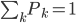 。
。
这样我们就有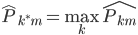 ,即主导类别占据该节点。
,即主导类别占据该节点。
定义1:我们的预测误差就是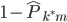 ,就可以定义
,就可以定义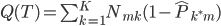 。
。
定义2:熵。我们定义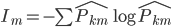 ,这样就可以定义
,这样就可以定义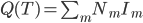 。
。
定义3: 基尼准则(Gini),定义函数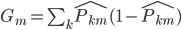 ,然后
,然后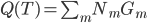 。
。
有了准则之后,我们就可以生长、剪枝和预测了。
为啥我觉得这就是决策树呢?喵了个咪的,就是一个质量定义问题嘛。回归和分类器之鸿沟一直延续呀,无论是线性模型还是树模型...
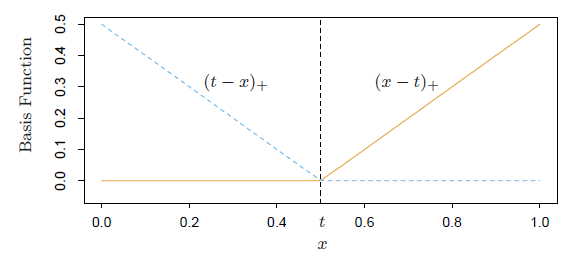
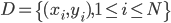 ,然后就是splines的思想:我们定义
,然后就是splines的思想:我们定义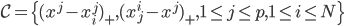 ,其中
,其中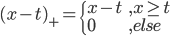 和
和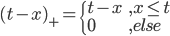 ,画出图形来就是:
,画出图形来就是: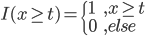 ,以及
,以及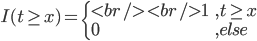 ,越来越有spines味道了是不是?
,越来越有spines味道了是不是?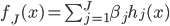 ,然后有意思的就来了:
,然后有意思的就来了: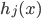 是
是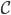 中函数或者几个函数的乘积,选定了
中函数或者几个函数的乘积,选定了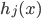 之后我们就可以用最小二乘法来求解相应的
之后我们就可以用最小二乘法来求解相应的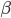 了。然后在接下来的每一步,我们都添加
了。然后在接下来的每一步,我们都添加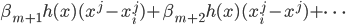 这样,一步步的,
这样,一步步的,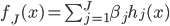 就开始增长。当我们用完了
就开始增长。当我们用完了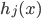 之后,显然有
之后,显然有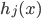 ——考虑移除那些对减少残差平方和贡献比较小的项目。沿着cross-validation的思路,就可以定义函数
——考虑移除那些对减少残差平方和贡献比较小的项目。沿着cross-validation的思路,就可以定义函数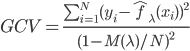 。
。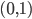 区间内任意的
区间内任意的 ,比如0.1,然后开始削皮~削皮的策略大概就是,选定一个维度,去掉这个维度比如最大10\%或者最小10\%的样本,然后看剩余部分的y均值有没有增长。总共有p个维度,所以我们有
,比如0.1,然后开始削皮~削皮的策略大概就是,选定一个维度,去掉这个维度比如最大10\%或者最小10\%的样本,然后看剩余部分的y均值有没有增长。总共有p个维度,所以我们有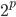 中削皮法。选择其中上升最高的方法,削皮。然后继续来一遍,直到不能再增长的时候,停止,最终得到一块“精华”(贪心的算法)。之后,我们又要开始粘贴,即再贴上去一块儿,看看是否能涨。这样我们得到一个
中削皮法。选择其中上升最高的方法,削皮。然后继续来一遍,直到不能再增长的时候,停止,最终得到一块“精华”(贪心的算法)。之后,我们又要开始粘贴,即再贴上去一块儿,看看是否能涨。这样我们得到一个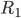 区,区域均值为
区,区域均值为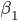 。
。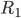 区中的样本,然后继续做下去,比如一共J次,得到J个区域(这些区域的空间可能是有交集的),这样的策略称为Bump-Hunting(肿块寻找),最终得到若干个区域,各区域中的样本均值作为
区中的样本,然后继续做下去,比如一共J次,得到J个区域(这些区域的空间可能是有交集的),这样的策略称为Bump-Hunting(肿块寻找),最终得到若干个区域,各区域中的样本均值作为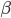 (以第一次出现的空间为准)。
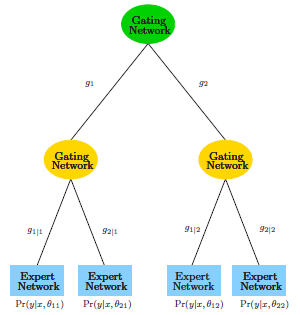
(以第一次出现的空间为准)。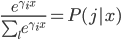 。对于最下面一层的expert
。对于最下面一层的expert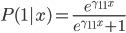 ,有点像logit的变形有没有?
,有点像logit的变形有没有?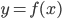 ,然后我们有参数模型
,然后我们有参数模型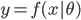 ,其中
,其中 ,
, 。
。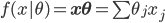 ,其中
,其中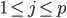 。显然,线性模型便是参数模型。
。显然,线性模型便是参数模型。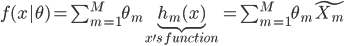 。说到底,就是已知的
。说到底,就是已知的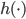 把数据从
把数据从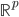 空间映射到一个新的
空间映射到一个新的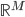 空间。然后还可以把y再广义化,用一个可逆的已知函数
空间。然后还可以把y再广义化,用一个可逆的已知函数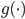 变成
变成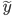 。这样,就有
。这样,就有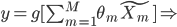
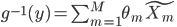 ,最终说来
,最终说来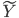 和
和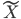 这两个空间实现了一种线性的映射关系。
这两个空间实现了一种线性的映射关系。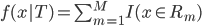 。显然这里
。显然这里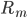 远非线性的,而且是变量。
远非线性的,而且是变量。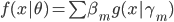 ,若
,若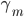 未知,即
未知,即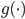 可变,则非GLM。这类的模型更适合的名字是:自适应基函数模型,即我们试图构造一些可以自适应的基函数,然后通过其线性组合构造最终的模型。这类模型经典如:树模型、GMM(高斯混合模型)、神经网络等。
可变,则非GLM。这类的模型更适合的名字是:自适应基函数模型,即我们试图构造一些可以自适应的基函数,然后通过其线性组合构造最终的模型。这类模型经典如:树模型、GMM(高斯混合模型)、神经网络等。