补上笔记。这节课讲的就是大名鼎鼎的Kernel Method...
核函数(正定)
定义 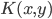 ,
, 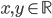 满足:
满足:
1) 对称: 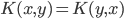
2) 正定: n个观测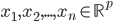 ,
,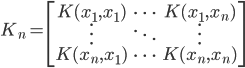 正定(或者非负定)。
正定(或者非负定)。
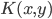 举例:
举例:
- 常数——
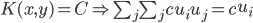
- 内积——
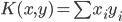 ,或广义下
,或广义下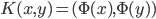 ,其中
,其中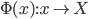 ,从
,从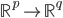 。
。
性质:
1. 封闭性
1) 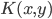 正定,
正定,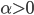 ,则
,则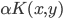 正定。
正定。
2) 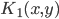 正定,
正定,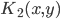 正定,则
正定,则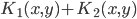 正定,
正定,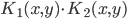 正定。
正定。
3) 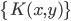 正定,
正定,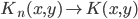 ,则
,则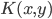 正定。
正定。
4) 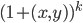 正定
正定
5) 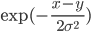 正定。
正定。
2. 归一性
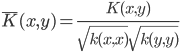 正定,
正定,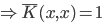 。
。
再生核Hilbert空间(RKHS)
(走神一下:关于这个命名的吐槽猛击 -> 翻译版、 英文原版Normal Deviate)
1. Hilbert空间:完备内积空间,可以视作欧氏空间的推广。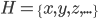 。
。
在这个空间中,我们定义:
- 加法:x+y
- 数乘:
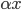 ,
, 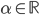 。
。 - 内积
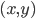 :对称性
:对称性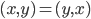 ;线性
;线性 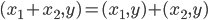 ,
,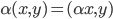 .
. - 零元素:若
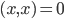 ,则
,则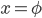 定义为零元素。
定义为零元素。 - 完备性:如果
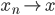 且
且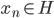 ,则
,则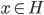 。(收敛到该空间内)。
。(收敛到该空间内)。
2. 再生核Hilbert空间
给定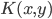 正定,可以构造Hilbert空间H使得
正定,可以构造Hilbert空间H使得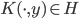 ,
,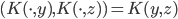 ;且构造一个
;且构造一个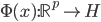 ,使得
,使得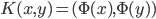 ,即核函数可以写成内积形式。
,即核函数可以写成内积形式。
这样对于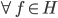 ,
,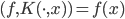 。
。
核方法
1. 基本思想
将线性模型推广到非线性模型的方法(其中较为简单的一种)
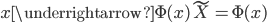 ,从
,从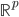 到
到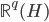 的一个映射。举例:
的一个映射。举例: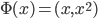 ,这样就可以拓展为广义线性模型。
,这样就可以拓展为广义线性模型。
2. SVM
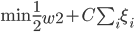
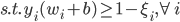
可以转化为:
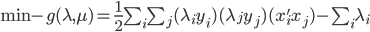
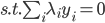
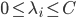
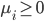
令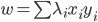 ,
,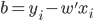 ,则
,则
非线性变换之后,
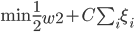
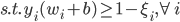
注意此时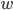 的维数有变化(
的维数有变化(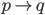 )。
)。
---------------------
如果各位更关心SVM后面的直觉,还是去看看Andrew Ng的相关课程吧...这里推导太多,直觉反而丢了一些。